Cколько обрезной доски в кубе — А-ЛесТорг

Для того, чтобы узнать сколько обрезной доски в кубе, в первую очередь нужно узнать каков объем одной доски.

Для определения объема (О) доски нужно располагать исходными данными:

Длина (Д)

Ширина (Ш)

Толщина (Т).

Формула для определения объема в этом случае имеет вид: О=Д*Ш*Т.

Мы же хотим узнать либо, сколько будет таких досок ( К, количество) в одном кубическом метре, либо какую площадь(П) можно закрыть досками того же суммарного объема.

Формулы для определения количества досок в одном метре кубическом.

К= 1 м.куб /О или К = 1 м.куб / (Д*Ш*Т).

Формулы, приведенные выше – равноценны, просто в первом случае вычисления выполняются поэтапно.

Для того, чтобы узнать площадь, которую можно настелить, израсходовав один кубический метр пиломатериалов достаточно разделить объем на толщину доски:

П=1м. куб./Т.

Но при расчете площади следует учитывать, что в действительности часть доски уйдет в обрезки.

Вычисления можно выполнить вручную, на калькуляторе, с помощью персонального компьютера. Особенно легко это делать в программе Excel.

Определенную сложность при проведении вычислений представляет собой перевод одних единиц измерений в другие. Длина может быть задана в метрах, а толщина или ширина в сантиметрах, иногда в миллиметрах. Перед вычислениями все значения нужно задать в метрах.

Итак, соотношения между единицами измерений:

1 см = 0,01 м

1 мм = 0,001 м

Что это значит? А это значит, что перед вычислениями следует измеренные в сантиметрах ширину или толщину уменьшить в 100 раз. Если были измерены или заявлены размеры в миллиметрах, то их нужно уменьшить в 1000 раз, то есть перенести десятичную запятую на три разряда влево. Пример: толщина обрезной доски составляет 22 мм. Это же толщина, выраженная в метрах – 0,022 м. В формулу для расчета нужно подставлять именно ее.

Попробуем практически произвести вычисления и узнать, сколько обрезной доски в кубе. Пусть имеем метр кубический доски с размерами: длина — 6 м, толщина – 22 мм, ширина 15 см.

Определим объем одной доски:

O = 6 м * 0,022 м * 0,15 м = 0,0198 м. куб.

Определяем количество досок в одном кубическом метре:

К= 1 м. куб. / 0,0198 = 50,5

Результат показывает, что в одном кубическом метре будет 50 целых досок и еще половинка, то есть еще одна доска в 3 м длиной.

Какую площадь можно настелить, израсходовав 1 м.куб. этой доски?

П=1 м.куб. / 0,022 м = 45,45 м.кв.

На самом деле, как уже указывалось выше, эта площадь будет меньше.

Учитывая относительно большую стоимость пиломатериалов, стоит повторять вычисления для того, чтобы убедиться в их правильности.

← Пол из обрезной доски
 | 
Строганная обрезная доска →

расчёты и определение по таблицам (видео)

Приобретение пиломатериалов сопровождается расчетами их количества. При этом большинство продавцов озвучивают стоимость дерева в кубометрах, особенно если вопрос касается того вида материалов, элементы которого не имеют строго одинаковых размеров. Рассмотрим, как можно вычислить количество досок при покупке одного куба обрезного материала.

Обрезная доска является важным материалом в строительстве. Ее необходимое количество измеряется кубометрами.

Расчет обрезной доски

Обрезной брус представляет пиломатериал с обработанными поверхностями. Калибры обрезного дерева лежат в пределах от 16 до 75 (толщина) и от 75 до 275 мм (ширина). Длина может соответствовать 3, 4 или 6 м.

Для определения того, сколько обрезной доски в кубе, можно воспользоваться простейшими математическими вычислениями.

Поскольку обрезные пиломатериалы имеют одинаковую геометрию, их число в кубе можно определить, посчитав объем одной единицы товара. Он равен произведению трех ее величин: ширины, толщины и длины.

Для правильности вычислений все измеренные величины необходимо перевести в метры. Полученное значение будет иметь вид десятичной дроби и будет числовой характеристикой объема единицы товара.

Поскольку приобретаемый товар имеет одинаковую ширину, толщину и длину, для определения его числа необходимо разделить 1 м³ на полученный объем единицы товара.

Приведем пример вычислений количества доски в кубе.

Таблица расчета кубатуры пиломатериала: доски обрезной, доски необрезной, рейки, бруска, вагонки и доски пола.

Допустим, приобретаются пиломатериалы 25 х 100 мм при стандартной длине 6 м.

1. Для расчетов переводим обозначенные величины в метры (пользуясь формулой 1 м = 1000 мм). То есть для перевода делим обозначенные параметры на 1000 (переносим запятую влево на три знака).

25 мм = 0,025 м

100 мм = 0,1 м

2. Выполняем умножение по формуле V (объем) = ширина х толщина х длина: 0,1 м х 0,025 м х 6 м = 0,015 м³
3. Определяем число обрезной доски в одном кубическом метре. Для этого делим 1 на полученное значение объема.

1 м /0,015 м = 66,66 штук.

Поскольку вам поставляются целые пиломатериалы, стоимость 66 штук будет немного меньше, чем одного куба дерева. Однако часто при продажах реализаторы принимают, что в одном кубе помещается только 66 штук размером 25х100 (длиной 6 м). На чем основаны такие ориентировочные расчеты не в пользу покупателя?

Определение количества обрезной доски по таблицам

Для тех, кто не хочет производить вычисления, разработаны таблицы (рис. 1).

В таблицах приведенные величины получены расчетами. В некоторых таблицах значения округлены, иногда такое округление производят сами продавцы. Так, число обрезного материла (размерами 25 х 100, 6 м) по округленным данным может составлять 66 штук (а не полученные при вычислениях 66,66 единиц товара).

Недостаток объема и небольшая переплата иногда компенсируется тем, что размер материала превышает оговоренные 6 метров (6,1 или 6,2 м). Такая компенсация неактуальна, когда в строительстве требуется обозначенная длина 6 м и лишняя пара сантиметров не играет роли.

Рисунок 1. Определение количества обрезной доски.

При покупке нескольких кубов дерева недостающие 0,66 единиц товара складываются в некоторое дополнительное количество, которые покупатель должен получить от продавца. Приведем пример.

Допустим, что покупатель приобретает в магазине или на рынке 5 кубометров пиломатериала (сечение 25 х 100, 6 м). По табличным данным, часто используемым продавцами дерева, покупатель должен получить 66 х 5 = 330 досок. На самом деле количество оплаченного товара равняется 66,66 х 5 = 333. 3 штук. То есть как минимум три половицы продавец должен добавить к определенному по таблице количеству.

Покупатель, приобретающий строительные материалы, должен выполнять собственные математические вычисления для проверки верности расчетов продавца. Правильные подсчеты делают честь поставщику строительных материалов и вызывают уважение у всех категорий покупателей, от индивидуалов до крупных застройщиков.

Существующие математические вычисления основаны на простейших формулах, изучаемых в разделе математики начальной школы.

Справиться с ними может любой образованный человек. Использование калькуляторов облегчает вычисления и делает их быстрыми, легкими и доступными.

Для взрослых, не справляющихся с проведением данных математических операций, рекомендуется обратиться к собственному ребенку для помощи. Если вашему сыну или дочери 10-11 лет, он вполне успешно справится с поставленной математической задачей.

20х100х2000, штук в одном метре по таблице

Деревянный забор не получится долговечным без знания некоторых тонкостей. Для строительства ограждения необходимо знать, сколько заборной доски в одном кубе. Такой подход поможет правильно рассчитать объем пиломатериалов и стоимость конструкции.

Доски для ограды из горбыля

Разновидность заборного сырья

Деревянные планки для забора производят из следующих пород деревьев:

• сосны;
• ели;
• дуба;
• лиственницы.

3 кубических метра доски 20х100х2000 для забора

Пиломатериалы предварительно просушивают в сушильных камерах. Заборные доски должны иметь коэффициент влагосодержания в пределах от 12 до 16 процентов.

Чтобы ограждение прослужило дольше, нужно правильно выбрать сырье. Рекомендуется брать прочные породы деревьев, таких как дуб, ясень, осина, акация.

Древесина лиственных пород используется редко. Пиломатериал из березы не подходит для заборной конструкции. Придется часто ремонтировать отдельные участки.

Способы монтирования ограждения

Все сооружения состоят из основных элементов:

• опор или столбов;
• каркаса;
• лицевого покрытия.

Два куба двухметрового штакетника

Обрезной пиломатериал применяется для возведения любых видов забора. Наиболее распространенные варианты:

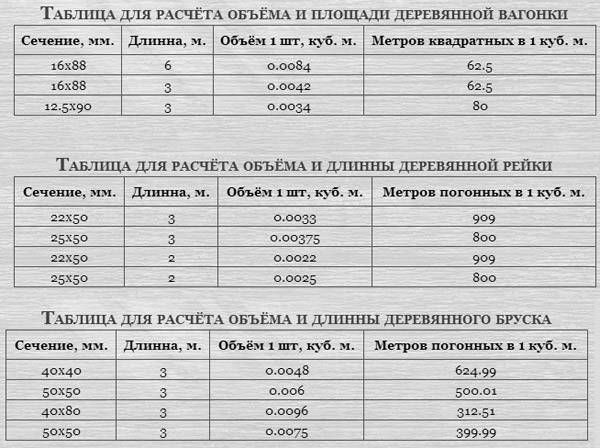
1. Лесенка (елочка) – паркетный метод монтирования заборных планок. Сооружают для двусторонних оград. К продольному каркасу под углом крепятся вертикальные или горизонтальные доски. Каждая планка ставится с небольшим зазором, перекрывая соседний элемент. Важная особенность: участок за забором не видно, хорошо пропускает воздух.
2. Штакетник – простая конструкция забора из досок. Планки монтируются к каркасу. Между элементами устанавливается определенный шаг. Крепятся доски с помощью гвоздей или саморезов. Преимущество конструкции: быстро возводится, не является материалоемким, смотрится эстетично.
3. Шахматка – две стороны забора имеют фасадный вид. Планки монтируются с зазором или без него в горизонтальном или вертикальном положении. Между секциями из досок устанавливаются столбы.
4. Решетка является декоративным забором. Монтируется в один-два ряда в виде скрещенных между собой элементов. Предварительно необходимо провести точные расчеты. Закупка производится с запасом досок на 10–13 процентов.

Необрезная доска для ограждения

Особенности проектирования и установки

Прежде чем закупать материал, рекомендуется выбрать вид забора. Предварительно производят замеры участка. Также следует учитывать ряд факторов:

1. Глубина опорных стоек составляет от 0,80 до 1,20 метра. Значение зависит от глубины промерзания почвы, пролегания грунтовых вод. Подземная часть столба обычно составляет ¼ части всей длины.
2. Столбы, находящиеся по углам периметра, в основании калитки и ворот, имеют наибольшую толщину.
3. Для увеличения площади опоры и жесткости столбы крепятся специальными башмаками.
4. Длина секций забора из доски не должна превышать 2,5 метра. Нужно учитывать нагрузку на несущий каркас, поскольку возможно провисание ограждения.
5. Следует определиться с высотой конструкции забора. Опоры не должны превышать верхней границы из досок более чем на 100 миллиметров.
6. Все заборные доски и деревянные элементы требуют дополнительной обработки защитными средствами.

Трехметровые обрезные планки

Планируя монтаж деревянного сооружения, важно вычислить, сколько в кубе заборной доски 2 метра.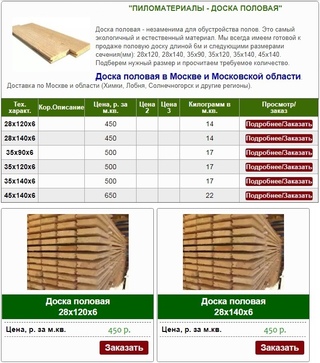 Пиломатериал размером 20х100х2000 мм обычно используют для возведения сооружения в качестве штакетника.

Сколько заборной доски в одном кубометре

Рассмотрим, как правильно выполнить расчет доски для забора. Планка характеризуется толщиной, шириной и длиной.

Сколько штук материала будет в одном кубе, зависит от размера.

Ниже приведены формулы для вычислений штакетника из доски толщиной 20, шириной 100 и длиной 2000 миллиметров (2 метра).

Объем пиломатериала (значения одной заборной доски переведены в метры кубические):

V = 0,02 * 0,1 * 2 = 0,004 куб. метра.

Полученная величина применяется в следующей формуле. N показывает, сколько в 1 кубе заборной доски 20х100х2000 мм:

N = 1 / 0,004 = 250 штук в метре кубическом.

Следующий показатель – площадь покрытия. Расчет доски заборной в м² выполняется по формуле:

S = 1,0 / 0,02 = 50,00 кв. м покрытия из 1 куба материала толщиной 20 мм.

При проведении вычислений все значения размеров доски для забора обязательно переводить в метры. Таблица, представленная ниже в статье, упростит расчеты.

Почему нужно знать, сколько требуется пиломатериалов

Вычисления производятся по следующим причинам:

1. Чтобы знать общую стоимость материала для будущей конструкции.
2. Общее количество досок для ограждения, и сколько штук в кубе.

В таблице приведены значения востребованных размеров сырья. Зная формулы, легко произвести вычисления самостоятельно.

Толщина доски, м	Ширина, метров	Длина, м	Покрываемая площадь 1 м3 пиломатериала, м2	Объем в 1 м3	Количество пиломатериала в 1 м3, штук
a = 0,02	b = 0,1	l = 2	S = 50	V = 0,004	≈ 250
		l = 3		V = 0,006	≈ 167
		l = 4		V = 0,008	≈ 125
		l = 6		V = 0,012	≈ 83
a = 0,025		l = 2	S = 40	V = 0,005	≈ 200
		l = 3		V = 0,0075	≈ 133
		l = 4		V = 0,01	≈ 100
		l = 6		V = 0,015	≈ 67
a = 0,03		l = 2	S = 33. 33	V = 0,006	≈ 167
		l = 3		V = 0,009	≈ 111
		l = 4		V = 0,012	≈ 83
		l = 6		V = 0,018	≈ 56

Преимущества деревянного ограждения

Важное достоинство – эстетичный вид. Есть и другие эксплуатационные показатели, делающие сооружения популярными:

1. Относительно невысокая трудоемкость.
2. Широкий выбор разновидностей конструкции.
3. Простота работ, не требуется специальная подготовка.
4. Доступность сырья.
5. Несложно производить ремонт.
6. Экологическая безопасность сооружения.

Трехметровые заготовки около частного дома

Привлекательный вид сооружения из двухметровых или трехметровых заборных досок могут сохранять на протяжении 10–13 лет. Пиломатериалы необходимо покрывать защитным слоем от неблагоприятных воздействий атмосферных осадков.

В магазинах представлен широкий выбор лакокрасочной продукции для заборов из деревянных досок. Составы позволяют уберечь от гнили и плесени, появления жучков. Часто дерево покрывают краской, которая не дает проникнуть влаге и защищает от повреждения поверхности.

Несмотря на широкий выбор сырья на строительном рынке для возведения ограждений, обрезная и необрезная деревянная доска пользуется спросом.

2-метровая доска для забора на даче

Мастеров привлекает простота в установке сооружения и невысокая цена по сравнению с профнастилом, декоративным камнем, кирпичом. Невысокая стоимость значительно влияет на выбор конструкции из натурального дерева.

Атрибутов и сетей куба

Сводка

Студенты будут использовать свои знания об атрибутах кубиков, работать вместе в группах и находить как можно больше кубиков.

Материалы

Дополнительные ресурсы

Книги

• Важная книга Маргарет Уайз Браун ISBN: 0064432270

Фон для учителей

Куб состоит из шести квадратных граней, двенадцати ребер и восьми вершин. Когда квадратные грани куба разделены по краям и разложены плоско, они образуют двухмерную фигуру, называемую сеткой.Для куба существует одиннадцать различных сетей.

• Сетка — двухмерная фигура, которую можно сложить в трехмерную фигуру, является сеткой этой фигуры.
• Лицо — плоская фигура, служащая одной стороной твердой фигуры. Грани куба — квадраты.
• Вершина (вершины) — точка, в которой два отрезка, линии или лучи встречаются, образуя угол.
• Ребро — отрезок прямой, на котором встречаются две грани твердого тела.

Сегодня ученики будут использовать свои знания об атрибутах кубиков, работать вместе в группах и находить как можно больше способов сделать куб. Двумерный узор для трехмерной формы называется сеткой.

Студенты будут работать вместе в небольших группах, и каждая группа будет разного цвета. Они будут использовать ленту, чтобы соединить фигуры, которые складываются в куб.

Предполагаемые результаты обучения

1.Продемонстрировать положительное отношение к математике.

2. Научитесь решать математические задачи.
3. Рассуждайте математически.

Инструкционные процедуры

Приглашение к учебе
Выведите учащихся на площадку. Спросите: «Кто может сказать, что такое атрибут? Атрибут описывает что-то в предмете или человеке. Попросите ученика встать перед классом и назвать атрибут ребенка (цвет его волос, глаз, обуви, и т.п.). Сегодня мы узнаем об атрибутах куба.

Прочтите книгу « Важная книга » Маргарет Уайз Браун.

Скажите студентам, что, как детективы, они будут описывать атрибуты куба.

Инструкционные процедуры

1. В качестве класса выберите в классе двух- или трехмерный объект (например, глобус или флаг). Попросите учащихся придумывать атрибуты, а учитель перечисляет атрибуты на доске.
2. Поднимите куб и обсудите со студентами различные атрибуты куба, убедившись, что они называют «боковые» грани. Попросите учащихся записать атрибуты в своих математических журналах.
   
3. Попросите учащихся осмотреть комнату и назвать предметы, имеющие форму куба. Проверьте заранее и убедитесь, что у вас есть хотя бы один или два кубических объекта в комнате! Если это не было затронуто, спросите учащихся, какие двухмерные формы составляют куб.
4. Затем просмотрите атрибуты куба.Запишите их на доске. Попросите учащихся записать их в своих дневниках.
5. Затем попросите учащихся объяснить, почему они считают, что форма куба важна. Попросите их придумать в реальной жизни предмет, имеющий форму куба, и перечислить его атрибуты. Попросите учащихся заполнить рабочий лист «Важная вещь». Заполнив лист, студенты могут составить буклет со своими атрибутами.
6. Затем учащиеся работают в группах по четыре человека, используя двухдюймовые квадраты, чтобы создать как можно больше различных сеток для куба.Дайте каждой группе два набора по 6 штук, чтобы у каждого в группе была возможность опробовать свои идеи. Как только они подумают, что у них есть сеть, попросите их доказать, что она работает, скопировав сеть на 2-дюймовую сетку, вырезав ее и сложив в куб. Возможно, вы захотите показать всему классу несколько первых рабочих сетей, которые являются Вы можете принять участие в соревновании, чтобы учащиеся сосредоточились. Побеждает группа с самыми разными сетками для куба.

Закрытие

В математических журналах пусть ученики подходят к классу и записывают атрибуты сетей.

• Каждая сетка состоит из шести квадратов, которые при правильном сложении образуют шесть граней куба.
• Для каждой сети шесть граней соединены пятью ребрами. Попросите учащихся поделиться и записать то, что они узнали о кубе.
• Кубики имеют двенадцать граней
• восемь вершин
• шесть граней

Оценка

• Ученики могут использовать миллиметровую бумагу, чтобы рисовать различные способы, которые они нашли для создания сети.
• Студент Важная книга о кубе.
• Записи в дневнике.
• Учащиеся создают буклет, демонстрирующий знание атрибутов куба.

Добавочные номера

Расширение учебной программы / адаптации / интеграция

• Отлично подходит для интеграции языковых навыков и письма в математику

Семейные связи

• Учащиеся отправляются на поиски «кубиков» у себя дома.

План оценки

Библиография

Основа исследования

Битти В., Коллинз Б. и Макиннес Б. (1997). Глубокое и поверхностное обучение: простая или упрощенная дихотомия? Бухгалтерское образование , 6 (1), 1-12.

Стихи глубокого обучения на поверхности или механическое заучивание имеют важное значение для учащихся, чтобы получить понимание для обучения.Процессы обучения студентов для глубокого обучения включают использование различных стилей обучения для улучшения личности студента.

Хартсхорн Р. и Борен С. (июнь 1990 г.). Практическое изучение математики: Использование манипуляторов. Вашингтон, округ Колумбия: Информационный центр ERIC по сельскому образованию и малым школам, ERIC Digest. (Номер услуги репродукции документов ERIC ED321967)

Активное участие в различных стилях обучения улучшит обучение студентов. Математика настолько абстрактна, что ученикам становится трудно ее понять.Следовательно, использование манипуляторов имеет важное значение для обучения.

Создано: 27.06.2006
Обновлено: 05.02.2018

114325

Запишите количество ребер, граней и вершин куба c-class-10-maths-CBSE

Подсказка: для решения этой задачи составьте диаграмму каждой фигуры и узнайте количество ее ребер, граней и вершин.

Полный пошаговый ответ:
$ \ Rightarrow $ Cube: —

В математике или в геометрии куб представляет собой твердую трехмерную фигуру, которая имеет 6 квадратных граней, 8 вершин и 12 ребер.Число ребер = 12
Число граней = 6
Число вершин = 8

$ \ Rightarrow $ Кубоид: —

Разница между кубом и кубоидом в том, что в кубе все ребра имеют одинаковую длину и все грани квадратные, но в кубоиде все грани не квадратные, могут быть и прямоугольники.
Число ребер = 12
Число граней = 6
Число вершин = 8
$ \ Rightarrow $ Конус: —

На диаграмме выше показаны конусы. Конус — это трехмерная форма в геометрии, которая плавно сужается от плоского основания (обычно круглого основания) к точке (которая образует ось к центру основания), называемой вершиной или вершиной.
Число ребер = 0
Число граней = 1
Число вершин = 0
$ \ Rightarrow $ Цилиндр: —

На диаграмме выше показан Цилиндр. Цилиндр — это одна из основных форм в математике, которая имеет два параллельных круглых основания на расстоянии (называемом высотой цилиндра).
Число ребер = 0
Число граней = 2
Число вершин = 0
$ \ Rightarrow $ Sphere: —

На диаграмме выше изображена сфера, которая имеет форму футбольного мяча.Сфера — это объект, который представляет собой абсолютно круглую геометрическую форму в трехмерном пространстве.
Число ребер = 0
Число граней = 0
Число вершин = 0
$ \ Rightarrow $ Треугольная пирамида: —

Диаграмма, показанная выше, представляет собой треугольную призму. Треугольная призма — это многогранник, состоящий из двух треугольных оснований и трех прямоугольных сторон. По определению, два треугольных основания параллельны и конгруэнтны друг другу.
Число ребер = 9
Число граней = 5
Число вершин = 6
$ \ Rightarrow $ Прямоугольная призма: —

Прямоугольная призма — это трехмерная форма.У нее шесть граней, и все грани призмы прямоугольные. Оба основания прямоугольной призмы должны быть прямоугольником. Также другие боковые грани будут прямоугольниками. Его еще называют кубоидом.
Число ребер = 12
Число граней = 6
Число вершин = 8

Примечание: всякий раз, когда вы сталкиваетесь с подобными проблемами, нарисуйте диаграммы и подсчитайте количество ребер, граней и вершин с помощью диаграммы. Такие действия решат вашу проблему и дадут вам правильный ответ.

Картонный куб

Справочная информация о твердых формах для учителей, родителей и опекунов

Эта страница предоставляет информацию, чтобы помочь педагогам и семьям обучать учащихся старших классов средней школы твердым формам. Он разработан для дополнения тематической страницы Solid Shapes на BrainPOP Jr.

.

Ваши дети, скорее всего, знакомы с основными двумерными плоскими фигурами, такими как квадраты, прямоугольники, круги и треугольники.Рекомендуем вместе посмотреть фильм «Формы самолета» в качестве обзора. Они могут иметь опыт работы с трехмерными твердыми телами из блоков, но могут не иметь словарного запаса для их описания и обсуждения. Вы можете опираться на их знания о твердых фигурах, которые представляют собой трехмерные фигуры, такие как кубы, прямоугольные призмы, пирамиды, цилиндры, конусы и сферы. Ваши дети должны уметь определять основные твердые формы и понимать их сходства и различия. Начните знакомить с фундаментальными понятиями и терминологией в геометрии, такими как вершины / вершины, ребра, грани и основания.Поощряйте своих детей находить вокруг себя простые твердые формы.

Кубики знакомы большинству детей. Пронумеруйте кубики или игральные кости, кубики льда, а некоторые коробки имеют форму кубиков. Куб имеет шесть плоских поверхностей или граней. Каждое лицо имеет форму квадрата с равной длиной сторон. Куб также имеет двенадцать ребер и восемь вершин. Напомните детям, что вершина — это угол фигуры. Форма множественного числа слова вершина — это вершин . Покажите своим детям различные примеры кубиков и помогите им определить грани, ребра и вершины.Прямоугольная призма — это сплошная фигура, у которой такое же количество граней, ребер и вершин, как у куба. Как следует из названия, грани прямоугольной призмы имеют форму прямоугольников. У некоторых прямоугольных призм есть грани, которые имеют форму прямоугольников и квадратов. Объясните детям, что куб — это особый вид прямоугольной призмы. Предложите детям найти примеры прямоугольных призм и указать на разные грани. Доски объявлений, коробки для хлопьев, коробки для обуви и книги — все это прямоугольные призмы.

Пирамида — это сплошная фигура, имеющая основание или основание и несколько треугольных граней. Основание пирамиды может быть разной формы, например прямоугольником, квадратом, треугольником или восьмиугольником. Стороны соединяются в одной вершине. У квадратной пирамиды есть основание, четыре стороны, восемь ребер и пять вершин. Скорее всего, ваши дети видели изображения Великих пирамид Египта. Вы можете нарисовать треугольные и прямоугольные пирамиды для своих детей, чтобы они могли видеть, что стороны всегда являются треугольниками, независимо от формы основания.

Цилиндр — это твердая форма, у которой есть две круглые грани, без ребер и без вершин. Цилиндр имеет изогнутую поверхность и может катиться. Банки из-под тунца, суповые банки, шесты и трубки — все это примеры цилиндров. Вы можете показать, как можно создать цилиндр, свернув прямоугольник в трубку и прикрепив к концам два круга. И наоборот, вы можете взять трубку от туалетной бумаги и разрезать ее вдоль, чтобы показать, что она может превратиться в прямоугольник. Помогите своим детям понять, что плоскими формами можно манипулировать, чтобы формировать твердые формы.

Конус — это твердое тело, имеющее одну изогнутую поверхность, без ребер и одну вершину. Транспортные конусы, воронки и рожки для мороженого — все это примеры конусов. Вы можете нарисовать разные примеры конусов, чтобы учащиеся увидели, как они могут различаться по размеру.

Шар — цельная фигура, знакомая всем детям. Шары, шарики и апельсины — все это сферы. У сферы нет грани, ребра и вершины. Сферы имеют изогнутую поверхность и могут катиться.

Изучение фигур, как двумерных, так и трехмерных, — это увлекательный способ для ваших детей исследовать окружающий мир.Как мы используем прямоугольные призмы каждый день? Из какой формы мы пьем? Поощряйте своих детей находить вокруг себя примеры твердых форм и задавать вопросы о том, как они их используют. Они бы предпочли играть в футбол, используя мяч или коробку? Почему?

Платоновых тел | 5 объяснений платоновых тел (видео + примеры)

Что такое платоническое твердое тело?

A Платоново тело — это правильный выпуклый многогранник в трехмерном пространстве с эквивалентными гранями, состоящими из конгруэнтных выпуклых правильных многоугольных граней.Этому критерию соответствуют пять тел: тетраэдр , куб, октаэдр, додекаэдр и икосаэдр .

Некоторые геометрические наборы бесконечны, как набор всех точек на линии. Платоновы тела, однако, представляют собой конечный набор всего из пяти трехмерных форм. Независимо от того, как вы смотрите на платоническое тело, лицо той же формы смотрит в ответ.

Свойства платоновых тел

Чтобы быть Платоновым телом, тестируемая форма должна:

• Быть выпуклым
• Будь трехмерным (многогранник)
• Имеют совпадающие лица
• Имеют совпадающие углы (вершины)

Содержание

1. Определение Платоновых тел

История пяти платоновых тел

Греческий философ Платон использовал уже существующую концепцию пяти идеальных тел, чтобы связать несовершенный реальный мир с идеальным миром своего воображения.Поскольку каждое из пяти тел имеет одну и ту же грань, независимо от того, как они вращаются, Платон использовал их в своем диалоге Тимей около 350 г. до н. Э. Он приписал четыре формы элементам (огонь, землю, воду, воздух) и додекаэдр небесам. Он организовал известную вселенную; в то время твердые тела всегда назывались Платоновыми телами в его честь.

Пять Платоновых тел

Вот пять Платоновых Тел и их отношения к двумерным формам:

1. Тетраэдр имеет четыре треугольные грани
2. Куб имеет шесть квадратных граней
3. Октаэдр имеет восемь треугольных граней
4. Додекаэдр имеет 12 пятиугольных граней
5. Икосаэдр имеет 20 треугольных граней

Никакие другие формы не могут быть созданы путем повторения только двумерного правильного многоугольника.Обратите внимание, что три из пяти твердых тел зависят от простоты и красоты равностороннего треугольника. Также обратите внимание, что количество граней всех Платоновых тел четное.

Еще одна интересная особенность Платоновых тел: их грани встречаются так, что три, четыре или пять граней соединяются в вершинах, образуя углы:

1. Тетраэдр имеет четыре вершины с тремя треугольными гранями, которые соответствуют
2. Куб имеет восемь вершин с тремя квадратными гранями, которые соответствуют
3. Октаэдр имеет шесть вершин с четырьмя треугольными гранями, которые соответствуют
4. Додекаэдр имеет 20 вершин с тремя пятиугольными гранями, которые соответствуют
5. Икосаэдр имеет 12 вершин с пятью треугольными гранями, которые соответствуют

Тетраэдр

От греческого, означающего четырехсторонний или четырехсторонний , эта форма представляет собой четыре равносторонних треугольника, соединенных по шести ребрам, чтобы образовать четыре вершины или угла.Это делает пирамиду прочной. Среди Платоновых тел только тетраэдр не имеет параллельных друг другу граней.

Куб

В переводе с греческого означает «шестигранный кубик», куб представляет собой шесть квадратов, соединенных по 12 ребрам, образуя восемь вершин. Он широко распространен в нашем современном обществе и известен людям тысячи лет. Кубики имеют три пары параллельных граней.

Октаэдр

От греческого восьмигранный или восьмисторонний октаэдр — это восемь равносторонних треугольников, соединенных по 12 ребрам, чтобы образовать шесть вершин или углов.У фигуры четыре пары параллельных граней.

Додекаэдр

В переводе с греческого означает двенадцатигранный , додекаэдр имеет 12 граней, образованных из пятиугольников. Они соединяются по 30 ребрам, образуя 20 вершин. В результате эта форма является второй по «округлости» среди Платоновых тел. У него шесть пар параллельных граней.

Икосаэдр

В переводе с греческого означает 20-гранный , икосаэдр состоит из 20 равносторонних треугольников, соединенных по 30 ребрам, образуя 12 вершин.Из-за относительно малых углов он наиболее близко приближается к сфере среди Платоновых тел. У него десять пар параллельных граней.

Использование платоновых тел

Поскольку Платоновы тела так хорошо соотносятся с числами, их формы часто появляются в виде игральных костей в настольных играх и других развлечениях, включая азартные игры. Куб, конечно, выглядит как кубики сахара, транспортировочные коробки, кубики льда и везде, где требуется легко упаковываемая, легко повторяемая форма.

Минералы часто образуют грубое приближение Платоновых тел:

• Тетраэдр: Тетраэдрит
• Куб: Галит, Пирит, Галенит
• Додекаэдр: Гранат
• Октаэдр: Флюорит, шпинель, алмаз

Удивительно, но молекулярные структуры также имитируют некоторые Платоновы твердые тела, либо естественным образом, либо благодаря химическим соединениям, созданным человеком:

• Тетра-трет-бутилтетраэдран
• Кубан
• Додекаэдран

Даже в микроскопическом мире есть примеры Платоновых тел.Вирусы, некоторые из мельчайших форм жизни, используют икосаэдр и куб для оптимизации своих жизненных функций. Двойные первооткрыватели ДНК, Уотсон и Крик, предсказали в своей работе такую ​​икосаэдрическую и кубическую симметрию.

Резюме урока

Теперь, когда вы проработали этот урок, вы можете идентифицировать и назвать пять Платоновых тел, указать идентифицирующие характеристики пяти Платоновых тел и связать эти пять Платоновых тел с их приближениями в реальной жизни.

Следующий урок:

Что такое многогранник?

Основы работы с платой

| Журнал WOOD

Позвольте зерну вести вас

Когда вы начинаете говорить о зерне, вы должны думать о бревне, из которого происходит заготовка. Концентрические кольца роста, видимые на концах бревна, образуют те полосы, часто дугообразные, которые вы видите на концах доски. Это отличительное зернистость торца обеспечивает удобную точку отсчета для определения шести плоскостей на доске.Когда толщина равна ширине, все четыре поверхности называются гранями.

Какими бы простыми ни казались кромка, поверхность и конец, возникает путаница, потому что эти плоскости на ложе могут не соответствовать условиям направления для детали. Например, на коробке с горизонтальным расположением волокон ссылки на передний и задний края концевой части будут указывать на концы вашей ложи. Итак, убедитесь, что вам ясно, относятся ли направления и такие термины, как край или конец, к заготовке или детали проекта.

Сохраняйте размеры в порядке

Измерения тоже могут привести к путанице.Размеры древесины обычно указываются в определенном порядке: толщина, ширина и длина (TxWxL). Толщина — это обычно наименьший размер на конце доски; ширина, размер по зерну; и длина, размер по или с зерном.

Если вы поменяете местами заданные размеры при вырезании детали для проекта, деталь подойдет, но может выглядеть неправильно. Изменение размеров также может повлиять на прочность или долговечность проекта. На рисунке внизу слева показаны три способа разрезания детали, просто изменив порядок размеров.

Словарь сокращений

Чтобы обрезать заготовку до нужного размера, плотники используют три основные операции распиловки, каждая из которых определяется в зависимости от направления волокон. Показаны следующие размеры:

Поперечный распил: Распиловка поперек волокон для уменьшения длины доски (также называется обрезкой). Поперечный надрез под углом, отличным от 90 градусов к краю доски, называется распилом под углом.

Распиловка: Распиловка в направлении волокон для уменьшения ширины доски. На пильный стол будет опираться поверхность или поверхность.

Повторная распиловка: Распиловка в направлении волокон для уменьшения толщины. Край обрабатываемой детали будет лежать на столе пилы.

Дополнительные термины, которые необходимо знать

Dado: Канал с плоским дном, проходящий поперек волокон, открытый от края до края.

Паз: Аналогичный канал, идущий с зерном. Ложа с пазом в ней иногда называют пахотной или пахотной.

Шпилька: Канал вдоль края или конца заготовки.

Фаска: Угол, вырезанный на части кромки, конца или грани.

Фаска: Угловой разрез по всей кромке, концу или поверхности.

Деформации и изменения размеров

При изменении влажности изменяется и размер куска дерева. Под воздействием высокой влажности древесина набухает и сжимается при понижении влажности. Это движение, степень которого варьируется у разных видов, также относится к зерну.

Только малейшие изменения размеров происходят с зерном или по длине.Но толщина и ширина могут значительно различаться. При переходе от зеленой к сушке в печи (стандарт испытаний, не путать с сушкой в ​​печи) некоторые виды древесины сжимаются почти на 13 процентов по ширине, или более чем на ³ ⁄ ₄
на штоке шириной 6 дюймов. Поскольку вы обычно строите проекты из высушенного материала, вы не испытаете таких экстремальных вариаций. Кроме того, после высыхания древесина не расширяется до такой степени при нормальных изменениях влажности.

Взгляд на торцевую поверхность волокон даст вам некоторое представление о том, как кусок дерева будет реагировать на влажность.Движение будет наибольшим в направлении полос или дуг или на по касательной к ним .

Радиальный рост и усадка — по дугам — будут меньше, вероятно, в диапазоне 40-80 процентов от тангенциального значения, в зависимости от вида. Эта неравномерная усадка может создавать напряжения в куске дерева, вызывая его деформацию.

4 обычных основы

Лук: Изгиб от конца до конца, в результате чего доска качается из конца в конец на одной стороне.

Crook: Изгиб края от конца до конца, в результате чего доска качается на одном крае.

Чашка: Изгиб от края до края, в результате чего доска качается из стороны в сторону на одной поверхности.

Twist: Деформация, приподнимающая один угол, в результате чего получается доска с непараллельными концами.

Проверяет и качает

Проверки (трещины на годовых кольцах) и встряски (трещины между годичными кольцами), показанные справа, также часто сопровождают коробление.И, конечно, если дела пойдут совсем плохо, вы можете найти доску, сочетающую в себе две или более разновидностей коробления.

Сколько граней у квадрата?

Сколько граней у квадрата ответ?

четыре кромки

5

4

У квадрата 12 граней?

У куба шесть граней, которые все являются квадратами, поэтому каждая грань имеет четыре равные стороны, а все четыре внутренних угла — прямые. См. Определение квадрата.У куба 12 ребер. Поскольку все грани квадратные и совпадают друг с другом, все 12 ребер имеют одинаковую длину.

Сколько ребер у квадрата?

Квадратная пирамида Лица 4 треугольника 1 квадрат Края8 Вершины5 Конфигурация вершины 4 (32,4) (34) 9

Есть ли у конуса ребра, грани или вершины?

У конуса одна грань, но нет ребер или вершин. Его лицо имеет форму круга. Поскольку круг — это плоская плоская форма, это лицо. Но поскольку он круглый снаружи, он не образует ребер или вершин.

Сколько граней у трехмерного квадрата?

12 граней

Всегда ли у трехмерных фигур больше краев, чем граней?

У куба 6 граней и 12 ребер, поэтому квадратная пирамида должна иметь 5 граней и 10 ребер. Количество ребер всегда вдвое больше количества граней. У трехмерных фигур всегда больше граней, чем граней.

Почему у трехмерных фигур всегда больше краев, чем граней?

Чтобы понять, как визуализировать грани, ребра и вершины, мы рассмотрим некоторые общие 3D-формы.У него все края одинаковой длины, потому что каждая грань представляет собой квадрат. Куб имеет: 6 квадратных граней, 12 прямых ребер и 8 вершин.

Какое трехмерное тело имеет на 4 ребра больше, чем вершин?

куб

Какое трехмерное тело имеет на 5 ребер больше, чем вершин?

Пентаэдр Название Вершины Края Квадратная пирамида (семейство пирамид) 58 Треугольная призма (семейство призм) 69

Может ли граф иметь больше ребер, чем вершин?

Граф с более чем одним ребром между двумя одинаковыми вершинами называется мультиграфом.В большинстве случаев, когда мы говорим о графике, мы имеем в виду простой неориентированный граф.

Какое трехмерное тело имеет 6 ребер или вершин?

Еще один примечательный момент: ваш ребенок также может узнать о базе. База — это особый вид лица. Цилиндры и призмы на самом деле имеют два основания, которые параллельны и конгруэнтны. Ребро — это линейный сегмент, на котором две грани пересекаются… .3-D тела: грани, ребра и вершины. 3D Solid ТРЕУГОЛЬНАЯ ПИРАМИДА (ТЕТРАЭДРОН) FACES4EDGES6VERTICES 48 дополнительных столбцов •

Каковы края трехмерной фигуры?

Края.Ребро — это место, где встречаются две грани. Например, у куба 12 ребер, у цилиндра — два, а у сферы — ни одного.

В чем разница между ребрами граней и вершинами?

Лицо — это плоская поверхность. Ребро — это место, где встречаются две грани. Вершина — это угол пересечения ребер. Множественное число — вершины.

Как вы считаете грани ребер и вершин?

2: 53 Предлагаемый клип 111 секунд Лица Края Вершины-3D Фигуры-Формула геометрии Эйлера… YouTube Начало предложенного клипа Конец предложенного клипа

Может ли многогранник иметь 10 граней, 20 ребер и 15 вершин?

Может ли многогранник иметь 10 граней, 20 ребер и 15 вершин? Следовательно, многогранник не может иметь 10 граней, 20 ребер и 15 вершин.