Какой пружинный матрас лучше выбрать: с зависимым или независимым пружинным блоком
Система пружин — важнейший параметр при выборе пружинного матраса. От нее зависят ортопедические качества, анатомичность, комфорт, а также выносливость будущей покупки. Блоки делятся на два типа: зависимые и независимые. Чем они различаются друг от друга, их преимущества и недостатки и какая конструкция предпочтительнее — читайте в нашей статье. И тогда у вас не останется никаких сомнений в том, какой лучше выбрать пружинный матрас: с независимыми или зависимыми пружинами!
Содержание статьи
- Из чего состоят пружинные матрасы
- Какие бывают пружинные блоки
- Сравнение
- Что же лучше?
- Итог
- Каталог
Из чего состоят пружинные матрасы
Как выглядит матрас внутри.
Как выглядит стандартный пружинный матрас в разрезе:
- Пружинный блок — важнейший элемент конструкции. Он принимает на себя всю нагрузку.
 Чем более совершенный блок в модели, тем лучше он к ней адаптируется, и тем больший вес он выдерживает.
Чем более совершенный блок в модели, тем лучше он к ней адаптируется, и тем больший вес он выдерживает. - Изолирующий слой для защиты наполнителей от контакта с пружинами. Чаще всего, это спандбонд или войлок. Слои материала располагаются с обеих сторон блока.
- Наполнители. Поверх изолирующего слоя расположены наполнители с различными свойствами. Жесткие материалы повышают ортопедичность, лучше распределяют вес тела на пружины, а мягкие адаптируются к изгибам тела. Чем выше слой наполнителя, тем комфортнее матрас.
- Чехол. От загрязнений и истирания матрасы защищены чехлом, который полностью закрывает конструкцию. Существуют модели с пышной стежкой для большего комфорта.
Примерно так выглядит обычный пружинный матрас. В редких случаях производители отступают от стандартной конструкции. Встречаются модели с двумя и тремя ярусами пружин, расположенными поверх друг друга, или односторонние модели — где настилочные слои в них расположены только с одной стороны.
Виды пружин
Все пружинные матрасы по конструкции подразделяются на две категории: зависимые и независимые. Последние тоже бывают на несколько типов — по количеству пружин на квадратный метр.
Зависимый блок пружин
Это известный всем блок Боннель, который состоит из металлической рамы (в некоторых моделях она отсутствует) и от 108 до 120 конусообразных пружин, которые соединены между собой. Блок сделан из прочной стали.
Плюсы
- Это недорогая конструкция. Покупатели могут сэкономить на блоке пружин и переплатить за более качественные наполнители или чехол. Самый дешевый матрас высотой 16 см обойдется всего в 6 122 ₽ за 80×200.
- Есть усиленный тип, дополненный блоками из пенополиуретана. Он выдерживает до внушительных 150 кг, когда как стандартный блок рассчитан на нагрузку около 90-120 кг.
- Как и беспружинные матрасы, он поддается скрутке для более удобной доставки. После того, как изделие примет обычную форму, им можно спокойно пользоваться.
 Скрутка никак не влияет на его характеристики. Обратите внимание — скрученный на производстве матрас скрутить обратно получится только с помощью специального пресса!
Скрутка никак не влияет на его характеристики. Обратите внимание — скрученный на производстве матрас скрутить обратно получится только с помощью специального пресса!
В 20 веке Bonnel был основой каждого пружинного матраса, но сегодня эта конструкция уходит в прошлое. Почему? Дело в его недостатках.
На фотографии хорошо видно, что элементы связаны друг с другом.
Минусы
- Не подходит для пар из-за эффектов волны и гамака. В первом случае партнеры будут чувствовать все колебания от движений спящего рядом человека. Любое движение будет отзываться колебанием пружин по всей площади. Если один партнер будет ворочаться, второй не сможет хорошо выспаться при всем желании. Во втором случае матрас будет сильно продавливаться под более крупным партнером, увлекая за собой соседние пружины. Спящий рядом начнет постепенно скатываться в его сторону. Разумеется, в этом случае о комфортном сне придется забыть.
- Не подходит для людей с большой массой тела.
 Пружинные блоки Боннель не выдерживают массу свыше 90-120 кг. В редких случаях производителям удается увеличить их выносливость, но таких матрасов ощутимо меньше, и стоят они дороже.
Пружинные блоки Боннель не выдерживают массу свыше 90-120 кг. В редких случаях производителям удается увеличить их выносливость, но таких матрасов ощутимо меньше, и стоят они дороже. - Главный минус — он не создает ортопедической спальной поверхности. Это обусловлено зависимой структурой пружин — они все связаны между собой. Достаточно надавить на одну, как соседние начнут сжиматься вслед на ней. Матрас с такими пружинами не будет в точности повторять контуры тела, особенно если верхний слой наполнителя тонкий.
- Маленький срок службы. Матрасы на блоке Bonnel не могут похвастаться долговечностью. Срок службы — около 5-7 лет.
Независимый пружинный блок
Это современная конструкция. Она состоит из отдельных пружин, которые не связаны друг с другом. Каждая упакована в чехол из спандбонда. Плотный нетканый материал защищает пружины и фиксирует их, позволяя сжиматься элементам только в вертикальной плоскости. В основу работы изделия с независимыми пружинами заложен принцип выравнивания тела за счет возможности разного уровня сжатия пружин под каждой областью. Это улучшает ортопедические характеристики блока и делает его долговечнее.
Это улучшает ортопедические характеристики блока и делает его долговечнее.
Независимые пружины мгновенно адаптируются к смене положения во время отдыха, отлично поддерживают тело, включая S-изгиб позвоночника. Поэтому на них так комфортно спать.
Правильная ортопедическая поддержка — главное условие здорового приятного отдыха.
Виды пружинных блоков: TFK, S1000 («Мультипакет»), S2000 («Микропакет»), DoubleSpring («Пружина в пружине»). Все они различаются количеством пружин и особенностями компоновки.
Несмотря на выбранную позу, матрас на базе независимых пружин создает правильную поддержку позвоночника — он остается ровным.
Плюсы
- Главный плюс — точечная поддержка тела. Сжимаются только те пружины, на которые воздействует вес. Это создает наилучшую поддержку тела, которая важна для здорового и комфортного отдыха.
- Существуют зональные матрасы с улучшенной ортопедической поддержкой. Вес в человечеством теле распространен неравномерно, некоторые его зоны давят на матрас сильнее.
 Например, бедра или плечи. Зональный блок усилен (больше витков проволоки, либо утолщенный профиль) в этих зонах. Такие модели рекомендуют людям с большим весом.
Например, бедра или плечи. Зональный блок усилен (больше витков проволоки, либо утолщенный профиль) в этих зонах. Такие модели рекомендуют людям с большим весом. - Идеален для семейных пар, потому что не передает колебаний от движений соседа. Можно ворочаться во сне сколько угодно и не беспокоиться, что любимый человек плохо выспиться.
- Подходят для подростков. Детям подросткового возраста уже можно спать на пружинных матрасах. Некоторые производители предлагают компромиссные варианты с уменьшенной высотой пружин в 10 см (стандартная высота — 14 см). Они подойдут ребятам с небольшой массой тела или для двухъярусных кроватей, которым не подходят высокие матрасы.
- Есть блоки пружин с увеличенной высотой в 18 см — TFK 18. Они сделают матрас выше без существенных переплат.
- Некоторые производители усиливают пружинные блоки цилиндрами из пенополиуретана либо по всей площади матраса, либо в тех зонах, где на матрас приходится увеличенная нагрузка.
 Таким образом производители улучшают ортопедические характеристики матрасов, делают их выносливее. Использование ППУ положительно скажется на долговечности матраса в целом. Такие пружины есть у Light Way и Hönnemed.
Таким образом производители улучшают ортопедические характеристики матрасов, делают их выносливее. Использование ППУ положительно скажется на долговечности матраса в целом. Такие пружины есть у Light Way и Hönnemed. - Некоторые пружинные изделия тоже продаются в упаковке со скруткой. Например, серия BeautyRoll
Минусы
- Высокая цена более продвинутых пружинных блоков, начиная с S1000. За комфорт приходится платить.
- С пружинными матрасами надо аккуратнее обращаться. Их категорически нельзя использовать в качестве батута или нагружать их сверх меры. Даже если одна пружина вылетит, о комфортном сне придется забыть.
Сравнение
Какой матрас лучше купить: с зависимым или независимым блоком?
Выбирая пружинный матрас, не забудьте уделить время настилочным слоям. От них тоже сильно зависит уровень комфорта отдыха.
Лучший выбор — изделия на независимых пружинах. Они обходят зависимые пружины по всем параметрам. Оптимальное количество элементов для эффективной ортопедической поддержки — 500 пружин на кв. м., что соответствует блоку S1000. Если вы ищите бюджетную модель, лучше обратить внимание на конструкции с блоком ТФК с 256 элементами на кв. м. По цене они сопоставимы конструкциям на системе Боннель.
Оптимальное количество элементов для эффективной ортопедической поддержки — 500 пружин на кв. м., что соответствует блоку S1000. Если вы ищите бюджетную модель, лучше обратить внимание на конструкции с блоком ТФК с 256 элементами на кв. м. По цене они сопоставимы конструкциям на системе Боннель.
Недорогой матрас на блоке Боннель можно приобрести в качестве временного спального места. Например, в гостевую комнату. В остальных случаях лучше выбрать модель на независимом блоке.
Вывод
На блоке пружин лучше не экономить, ведь он центр конструкции матраса. От него напрямую зависит комфорт и польза сна.
Специалисты МногоСна рекомендуют сделать выбор в пользу модели на независимом блоке. Сегодня бюджетные изделия на блоке TFK стоят практически столько же, сколько модели на зависимом блоке Боннель. Выбор очевиден.
Что такое блок независимых пружин?
Пружинные блоки, используемые в производстве матрасов, делятся на два типа: независимые и зависимые. Классический зависимый пружинный блок обычно называется «Боннель». Принцип его действия мы можем наблюдать в обычных недорогих диванах. Самый главный минус «Боннеля» — жесткая сцепка одной пружины с другой. Таким образом, продавливается целый ряд пружин и даже те, на которые не идет никакая нагрузка, и возникает так называемый «эффект гамака». Такой эффект нежелательно действует на позвоночник и создает дискомфорт во время сна и отдыха, особенно людям с большим весом.
Классический зависимый пружинный блок обычно называется «Боннель». Принцип его действия мы можем наблюдать в обычных недорогих диванах. Самый главный минус «Боннеля» — жесткая сцепка одной пружины с другой. Таким образом, продавливается целый ряд пружин и даже те, на которые не идет никакая нагрузка, и возникает так называемый «эффект гамака». Такой эффект нежелательно действует на позвоночник и создает дискомфорт во время сна и отдыха, особенно людям с большим весом.
Зависимые пружины «Боннель»
На смену классическому блоку зависимых пружин пришел блок независимых пружин. Самый популярный блок носит название TFK, которое произошло от немецкого «Taschen Feder Kern», он, кстати, и был разработан немецкими специалистами. Если переводить это название дословно, то получится что-то типа «пружины в мешочках». А все потому, что каждая пружина имеет свой индивидуальный чехол из прочной ткани (обычно используется спанбонд). Пружины не имеют жесткой связи друг с другом, а для того, чтобы каждая пружина «сидела на своем месте» чехлы крепко спаиваются друг с другом. Таким образом, достигнуто самое важное — независимость хода пружин. Такие пружины способны воспринимать нагрузку очень точечно: продавливаются только пружины, на которые идет непосредственная нагрузка, а соседние остаются в разжатом состоянии.
Таким образом, достигнуто самое важное — независимость хода пружин. Такие пружины способны воспринимать нагрузку очень точечно: продавливаются только пружины, на которые идет непосредственная нагрузка, а соседние остаются в разжатом состоянии.
Блок независимых пружин TFK
Независимые пружины обладают высоким ортопедическим эффектом и способны выдерживать большие нагрузки. Классический блок TFK содержит 256 пружин на 1 квадратный метр, этого достаточно для получения должного эффекта и прочности. Но существуют также блоки с увеличенным количеством пружин, они носят название S1000 и S2000. Заглавная буква «S» означает «spring», что в переводе с английского означает «пружина».
Блок независимых пружин S1000 содержит 500 пружин на один квадратный метр. Почему 500, а не 1000? В Европе принято считать количество пружин на одно спальное место, за которое берется 2 квадратных метра. Пружины в S1000 имеют меньший диаметр, чем в блоке TFK, за счет чего также увеличивается точечное восприятие нагрузки. Блок S1000 называют также Multipocket.
Блок S1000 называют также Multipocket.
Самый мощный из независимых пружинных блоков S2000 (Micropocket) состоит из 1000 пружин с малым диаметром. S2000 способен выдерживать огромные нагрузки и большое давление, а также обладает самым высоким уровнем ортопедической поддержки человеческого тела.
И в заключение небольшой совет: не стоит экономить на своем сне и здоровье. Матрасы на зависимых пружинах, как правило, покупаются на съемные квартиры или в гостиницы для того, чтобы получить дешевый пружинный матрас.
Блок независимых пружин TFK — самый недорогой из этой серии, а S1000 стоит ненамного дороже, но эффект уже увеличен вдвое. S2000 — на нем обычно построены матрасы премиум-класса с высоким уровнем комфорта и анатомичности. Любой блок независимых пружин хорошо подходит парам с большой разницей в весе.
Выбрать матрас
Независимые и зависимые пружинные блоки, что выбрать?
- Где я:
- Главная
- Полезная информация
- Независимые и зависимые пружины в чем разница?
Каждый ортопедический матрас классического типа обладает таким устройством, как пружинный блок. Он является одной из важнейших составляющих, поскольку именно от его конструкции и качества зависит не только комфорт во время сна, но и здоровье позвоночника.
Он является одной из важнейших составляющих, поскольку именно от его конструкции и качества зависит не только комфорт во время сна, но и здоровье позвоночника.
Существуют также беспружинные матрасы, особенности и стоимость которых несколько отличаются от пружинных аналогов. О них мы более подробно поговорим в других статьях.
Кропотливое производство
На изготовление пружинного блока (особенно если речь идет о высококачественной конструкции) затрачивается немало времени, средств и сил. Пружинное устройство требует не только наличие профессионального оборудования, но и тщательный контроль производства на каждом этапе, начиная от выбора материалов и процесса навивки пружин до проверки качества готового изделия. Только при строгом соблюдении всех этих условий можно получить на выходе первоклассный матрас с независимым блоком пружин. Технология изготовления зависимых конструкций несколько проще.
Зависимые пружины – «дешево и сердито»
Матрасы с зависимым пружинным блоком – практичный вариант для тех, кто желает сэкономить. Стоимость таких изделий существенно ниже, чем у независимых аналогов, но и функциональные качества, соответственно, прямо пропорциональны цене.
Стоимость таких изделий существенно ниже, чем у независимых аналогов, но и функциональные качества, соответственно, прямо пропорциональны цене.
В матрасах с зависимой конструкцией все пружины соединены между собой металлической проволокой. В результате такого устройства небольшой участок матраса, на который осуществляется давление, тянет за собой вниз все соседние области. Приемлемый комфорт во время сна в данном случае обеспечивается, а вот сохранение здоровья позвоночника уже находится под вопросом.
Независимые пружины – «ваша спина скажет вам спасибо!»
Совсем другое дело – матрасы с блоком зависимых пружин. В таких изделиях каждая пружина находится в отдельном чехле, благодаря чему нажим на один элемент не влечет за собой продавливание остальных. Матрасы в основе которых установлены независимые пружины, создают идеальные условия для позвоночника, обеспечивая его правильное положение, что является залогом комфортного и глубокого сна, а также здоровья спины и отменного самочувствия утром.
Выбирая между независимыми и зависимыми пружинными блоками, не забывайте, что не стоит экономить на самом ценном в нашей жизни – здоровье, ведь, как говорится, «будет здоровье – будет всё!».
Что такое блок независимых пружин?
Независимый пружинный блок в современных матрасах – это комфортный сон, выраженный ортопедический эффект и продолжительная эксплуатация. Зная все преимущества такой конструкции, можно сделать правильный выбор и обеспечить себе здоровье и полноценный отдых.
Независимые пружины для матрасов были разработаны несколько десятилетий назад – и уже сегодня во всем мире получили широкую популярность. Зная их особенности, преимущества и виды, можно с легкостью понять, как выбрать матрас с блоком независимых пружин и обустроить спальное место, полностью соответствующее всем потребностям и пожеланиям владельцев.
Классификация матрасных пружинных блоков
Первые пружинные матрасы появились еще в конце 19 века. Современные пружинные матрасы очень популярны и востребованы, несмотря на появление множества беспружинных вариантов. На сегодняшний день создано два типа блоков – зависимый и независимый, и у каждого есть свои особенности.
Современные пружинные матрасы очень популярны и востребованы, несмотря на появление множества беспружинных вариантов. На сегодняшний день создано два типа блоков – зависимый и независимый, и у каждого есть свои особенности.
Зависимый пружинный блок
Система пружин известная сегодня как «боннель», была запатентована в 1883 году Джозефом Леггетом – и с тех пор не претерпела практически никаких изменений. Под этим названием скрывается известный во всем мире зависимый пружинный блок.
«Боннель» представляет собой комплекс из сцепленных между собой четырехвитковых или пятивитковых пружин, соединенных между собой по всей длине. Пружины имеют биконусную форму – сужаются к центру и расширяются к краям, что обеспечивает дополнительную упругость и поддержку. Матрасы с зависимым блоком долго оставались единственным возможным вариантом, однако со временем выявились и недостатки системы – излишне сильная деформация спального места при большой нагрузке из-за плотной зависимости элементов и появление дискомфорта по мере изнашивания пружин.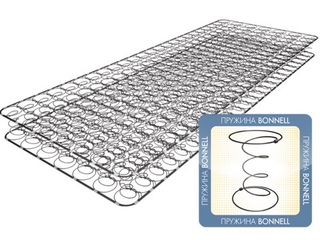 Все это побудило специалистов разработать новый вариант пружин.
Все это побудило специалистов разработать новый вариант пружин.
Независимый пружинный блок
В основе блока данного типа лежит так называемая карманная технология. Каждая пружина в такой системе упакована в отдельный чехол или «караман» и никак не соприкасается с соседними элементами. Благодаря этому все части конструкции работают автономно, реагируя только на нагрузку, которой подвергаются они сами. Это позволило избежать «эффекта гамака», характерного для зависимого блока, и обеспечить максимально комфортную поддержку тела во сне.
Особенности конструкции независимого блока
Понять, что такое независимый пружинный блок, и почему его стоимость настолько высока, также позволит знание особенностей его конструкции.
- Материалы высокого качества. Для пружин используют специальную высокоуглеродистую сталь, для чехлов – особый нетканый материал, что обеспечивает длительную эксплуатацию матраса без потери свойств.
- Различные типы пружин. В независимом блоке могут быть цилиндрические, биконусные и бочкообразные пружины на 4,5 или 6 витков.
 Чем больше количество витков, тем комфортнее поддержка.
Чем больше количество витков, тем комфортнее поддержка. - Большое количество элементов. Блок независимых пружин может насчитывать до 1000 элементов на квадратный метр. Чем больше данное число, тем выше жесткость матраса.
Разработка такой системы включает немало инновационных решений и требует значительных материальных и временных затрат. Именно это и объясняет более высокую стоимость моделей.
Преимущества матрасов с независимым пружинным блоком
Многочисленные отзывы подтверждают следующие преимущества матрасов с независимыми пружинами:
- оптимальная поддержка и комфорт;
- способность выдерживать высокие нагрузки;
- долгий срок службы – не менее 10 лет;
- коррекция проблем с позвоночником, снижение болей в мышцах и суставах;
- быстрое восстановление тела и полноценный отдых;
- отсутствие шумов и скрипов, характерных для зависимого блока.
Минусы матраса с блоком независимых пружин
Недостатки данных моделей достаточно малочисленны и в основном субъективны. К ним относят:
К ним относят:
- Дороговизна. Матрас с блоком независимых пружин действительно отличает высокая цена, которая обусловлена значительным уровнем комфорта и особыми технологиями производства. В то же время экономить на здоровье не стоит – а приобрести такой матрас можно со значительной скидкой, которую нередко предлагают магазины.
- Быстрый износ. Проблемы с нарушением функций пружин могут быть связаны с низким качеством товара или неграмотной эксплуатацией с недопустимыми нагрузками. Однако в большинстве случаев такие модели демонстрируют высокую надежность.
- Дискомфорт. Неудобства обычно вызваны некорректным выбором типа пружин и степени жесткости матраса. Стоит тщательно тестировать понравившуюся модель перед покупкой.
Виды независимых пружинных блоков
Чтобы правильно подобрать и купить матрас с независимыми пружинами, необходимо представлять себе особенности каждого типа конструкции. Сегодня в Москве можно найти спальные принадлежности со следующими видами блоков:
- Pocket Spring или TFK – Taschen Feder Kern.
 Наиболее популярная разновидность блока. Состоит из 6-витковых пружин в виде бочонка количеством до 300 штук на квадратный метр. Обладает выраженными ортопедическими свойствами.
Наиболее популярная разновидность блока. Состоит из 6-витковых пружин в виде бочонка количеством до 300 штук на квадратный метр. Обладает выраженными ортопедическими свойствами. - Multipocket или S1000. В основе блока – цилиндрические пружины малого диаметра до 4 см на 10-12 витков, количество – 500-1000 шт/м2. Обладает высокой упругостью, способен поддерживать тело в естественном положении.
- Micropocket или S2000. Система независимых цилиндрических элементов диаметром всего 2,5 см на 12-14 витков количеством 500-1000 шт/м2. Оптимальна для людей с большим весом и тех, кому для сна требуется поверхность с высокой жесткостью.
- Hour Glass «Песочные часы». Блок с пружинами соответствующей формы. Диаметр – до 6 см, количество – не более 300 шт/м2. Система устойчива к постоянно меняющимся нагрузкам, а матрас с таким блоком обладает умеренной упругостью, хорошими ортопедическими свойствами и комфортной поддержкой.
- Dual Spring «Пружина в пружине». Блок состоит из элементов цилиндрической формы диаметром приблизительно 6 см, количество – 256 шт/м2.
 Рекомендован для пар с большой разницей в весе и обладателям солидной массы тела.
Рекомендован для пар с большой разницей в весе и обладателям солидной массы тела. - DualZone и MultiZone. Матрасы с продольными и поперечными зонами жесткости соответственно. Содержат блоки с различным количеством и свойствами пружин, рекомендуются для семейных пар с различными потребностями и большой разницей в весе, а также для людей, имеющих проблемы с позвоночником.
Если знать основные типы конструкции, можно значительно быстрее определить, как выбрать блок независимых пружин. Однако тем, кто не слишком уверен в своих знаниях или имеет определенные проблемы со здоровьем, обязательно необходимо проконсультироваться с компетентным сотрудником магазина или лечащим врачом перед покупкой.
Что выбрать: пружинный блок или ППУ?
Один из основных вопросов, который стоит при выборе дивана: это какой диван выбрать — с пружинным блоком, или с ППУ?
Вначале кратко разберемся, какие пружинные блоки бывают, чем они отличаются, как проявляются в них ортопедические свойства, какие мягче, какие удобнее, и какие надежнее.
Самый первый пружинный блок, который используется в диванах уже на протяжении столетий – пружинный блок с красивым названием «бонель». Пружинный блок этого типа назвается зависимым, т.к. пружины сверху и снизу скреплены с соседними пружинами при помощи горизонтальных параллельных спиралей (эти спиральки представляют собой длинный тонкие пружинки). Вся конструкция по периметру прикрепляется к достаточно толстой окантовочной металлической проволоке или к плоской металлической рамке. Все это изготовлено из высокоуглеродистой пружинной стали, часто из нержавеющей. В результате при нагрузке на какую-либо одну пружину, сразу задействуются соседние пружины, тем самым распределяя нагрузку и не давая пружинам проминаться до конца. Этот пружинный блок очень надежен, и практически вечен. Мягкость дивана на основе этого пружинного блока зависит напрямую от того, какого диаметра была использована проволока для производства пружин. Но это не самое главное в диване. Самое главное в диване – это то, чем закрывается этот пружинный блок. От того, насколько качественные материалы используются при изготовлении «бутерброда» на основе пружинного блока, зависит комфорт и долговечность дивана. Чаще всего пружины закрываются жестким войлочным матом, этот мат не дает пружинам выступать из дивана, и человек не ощущает их. Но мат достаточно жесткий, и сидеть на нем было бы некомфортно, поэтому далее используется чаще всего ППУ (пенополеуретан – мебельный поролон), он и придает окончательную мягкость. Иногда в этом «сэндвиче» используется прослойка на основе кокосовой койры, при продаже дивана при этом пишут: диван с «кокосом» — положительные свойства от этого не улучшаются, лишь повышается жесткость – но как рекламный ход всем нравится. Ну и все это покрывается мебельной тканью, которая принимает на себя внешнюю нагрузку, и должна быть износостойкой и не пачкающейся. Вывод: качество дивана на основе пружинного блока определяется не блоком (он стальной и практически не подвержен износу), а теми материалами, в которые он закрыт: это ткань, ППУ и войлочный мат.
От того, насколько качественные материалы используются при изготовлении «бутерброда» на основе пружинного блока, зависит комфорт и долговечность дивана. Чаще всего пружины закрываются жестким войлочным матом, этот мат не дает пружинам выступать из дивана, и человек не ощущает их. Но мат достаточно жесткий, и сидеть на нем было бы некомфортно, поэтому далее используется чаще всего ППУ (пенополеуретан – мебельный поролон), он и придает окончательную мягкость. Иногда в этом «сэндвиче» используется прослойка на основе кокосовой койры, при продаже дивана при этом пишут: диван с «кокосом» — положительные свойства от этого не улучшаются, лишь повышается жесткость – но как рекламный ход всем нравится. Ну и все это покрывается мебельной тканью, которая принимает на себя внешнюю нагрузку, и должна быть износостойкой и не пачкающейся. Вывод: качество дивана на основе пружинного блока определяется не блоком (он стальной и практически не подвержен износу), а теми материалами, в которые он закрыт: это ткань, ППУ и войлочный мат.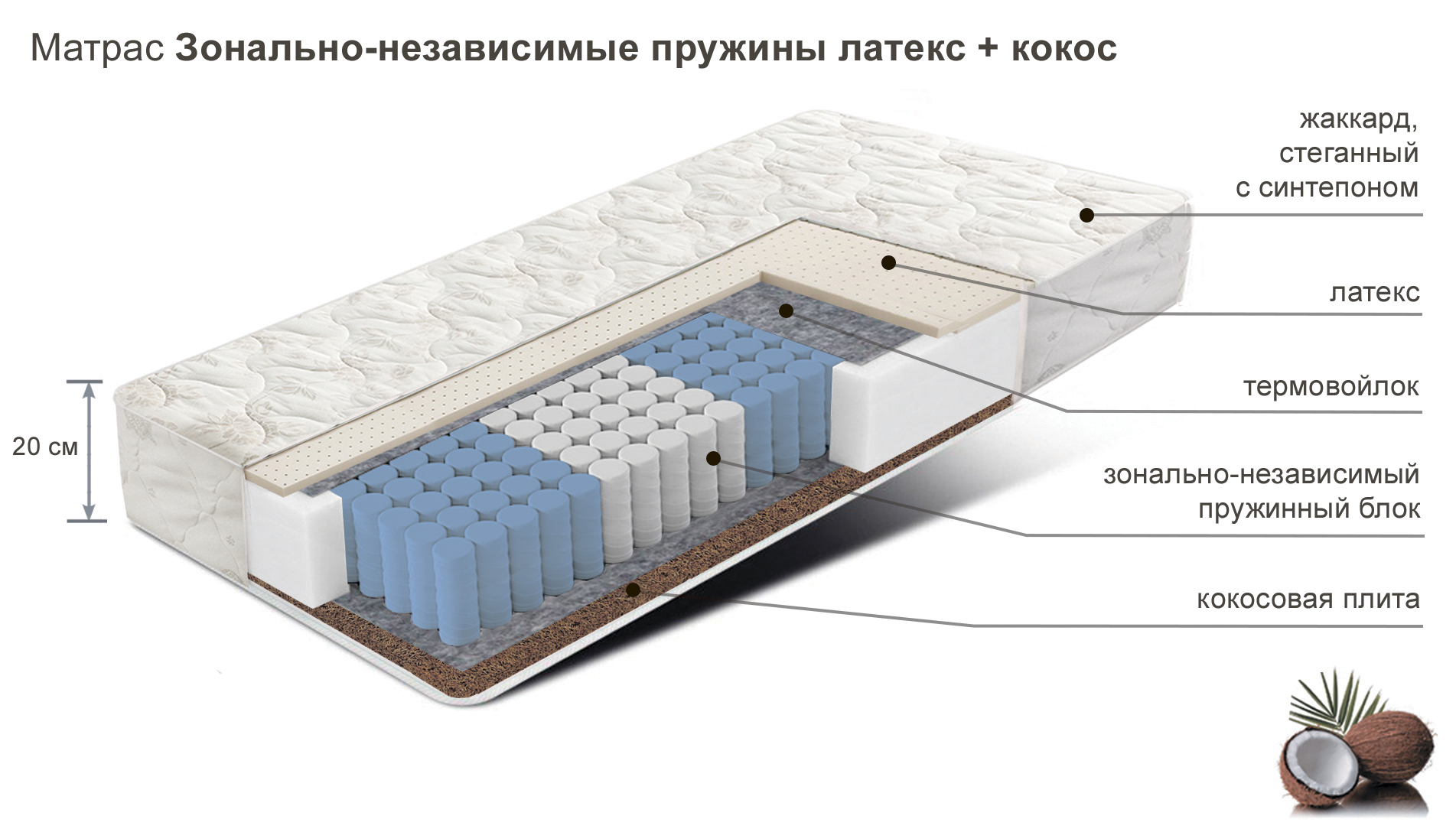
Независимый пружинный блок: это блок на основе пружин не связанных жестко друг с другом. В нем каждая пружина заключена в тканевый мешочек, который соединен с другими в нескольких точках. В этом пружинном блоке продавливается только та пружина, на которую приходиться нагрузка, соседние пружины при этом задействуются минимально. При изготовлении дивана пружинный блок на основе независимых пружин тоже покрывается слоем укрывающих его материалов. Мягкость этого пружинного блока тоже зависит от толщины пружинной проволоки. Качество блока на основе независимых пружин определяется количеством пружин на квадратный метр – чем их больше – тем лучше. Может быть «независимый» пружинный блок немного комфортнее чем «зависимый», но он менее надежен, и качество его изготовления очень сильно влияет на его надежность. Поэтому выбирая диван с «независимым» пружинным блоком желательно знать кто его производитель: если большая надежная компания – это хорошо, а если непойми кто – это плохо, и лучше предпочесть в таком случае обычный «зависимый» — он не подведет.
ППУ – пенополеуретан – в простонародье поролон. Это современный упругий материал. При его производстве ему можно задавать необходимые свойства. И это широко применяется при изготовлении мягкой мебели. ППУ можно сделать более жестким или мягким, упругим или не очень, можно при помощи присадок увеличить его срок службы во много раз. При этом удобство у такого ППУ будет даже выше чем у независимого пружинного блока, а срок эксплуатации гораздо дольше. Так же ППУ позволяет изготавливать диваны такой формы, в которой применение пружинного блока невозможно или нежелательно. Но ППУ ППУ рознь, и если в диване будет применен дешевый «поролон», то этот диван быстро «просядет» и станет некомфортным. Но если диван сделан на хорошей фабрике, то практически гарантированно, что ППУ там настоящий, мебельный. Он легко выдерживает любые нагрузки, быстро восстанавливает свою форму, и очень долговечен.
Что же выбрать: пружинный блок или ППУ? Это решать Вам. И тот и другой материал одинаково качественен, если изготовлен хорошо. Поэтому лучше остановить выбор на производителе с хорошей репутацией, тогда и пружинный блок и ППУ будут хорошим выбором, прослужат долго и будут приятны в эксплуатации. Так же желательно посидеть на диване перед покупкой – этим Вы сами определите – подходит ли он Вам. Кому то нравится пожестче, кому то помягче. Кому то нравиться чтобы диван, когда на него садишься, «проваливался», а некоторым хочется, чтобы он держал форму. Все вкусы разные, а выбор ППУ или пружинный блок не важен, так как это всего лишь инструменты, с помощью которых производители добиваются необходимого эффекта при производстве мягкой мебели. Главное – надежный, проверенный временем производитель.
Поэтому лучше остановить выбор на производителе с хорошей репутацией, тогда и пружинный блок и ППУ будут хорошим выбором, прослужат долго и будут приятны в эксплуатации. Так же желательно посидеть на диване перед покупкой – этим Вы сами определите – подходит ли он Вам. Кому то нравится пожестче, кому то помягче. Кому то нравиться чтобы диван, когда на него садишься, «проваливался», а некоторым хочется, чтобы он держал форму. Все вкусы разные, а выбор ППУ или пружинный блок не важен, так как это всего лишь инструменты, с помощью которых производители добиваются необходимого эффекта при производстве мягкой мебели. Главное – надежный, проверенный временем производитель.
Зависимый пружинный блок Боннель (Bonnell): преимущества и недостатки
Зависимый пружинный блок Боннель (Bonnell) является одним из первых, появившихся в производстве матрасов и диванов и вот уже около 150 лет, он пользуется огромной популярностью у потребителей. Конструкция блока состоит из пружин биконусной формы с 5-ю витками, которые фиксируются «замками». «Замок» из стальной высокоуглеродистой пружинной проволоки диаметром 1,4 мм на первом и пятом витке пружины не позволяет ей самопроизвольно раскручиваться и выкручиваться.
«Замок» из стальной высокоуглеродистой пружинной проволоки диаметром 1,4 мм на первом и пятом витке пружины не позволяет ей самопроизвольно раскручиваться и выкручиваться.
Благодаря этой технологии и появилось название «зависимый пружинный блок»: каждая пружина работает как один механизм — при нагрузке, сдавливаются не только те пружины, на которые приходится давление, но и соседние.
Пружины зависимого блока Боннель (Bonnell) изготовлены из высококачественного стального сплава. Витки имеют различный диаметр: первый и пятый витки имеют наибольший равный диаметр, второй и четвертый равный диаметр, но меньше чем два предыдущих, а третий (средний) виток по диаметру меньше, чем все выше перечисленные. Такая навивка пружин позволяет с легкость входить одному витку в другой и практически не издавать шума при работе всего пружинного блока под нагрузкой. В матрасах компании «АСАНА» используются пружины толщиной 1,8 мм.
Пружины после изготовления проходят термическую обработку, которая снимает остаточную напряженность и придает пружинному блоку упругость и долговечность.
Матрасы на зависимом пружинном блоке Боннель (Bonnell) обладают как ортопедическими, так и анатомическими свойствами. Преимуществом таких матрасов является низкая цена и длительный срок службы. Они идеально подойдут для гостевой спальни, дачи, съемных квартир и гостиниц. Довольно часто матрасами на зависимом пружинном блоке Боннель (Bonnell) комплектуются и недорогие кровати.
Матрасы на зависимом пружинном блоке Боннель (Bonnell) содержат 112 пружин на 1 квадратный метр (225 пружин на спальное место) и рассчитаны на средний вес спящего человека.
Внутри матраса находится большой объем воздуха, благодаря чему изделие хорошо вентилируется и быстро высыхает при намокании. При тщательном уходе и соблюдений правил эксплуатации матрас прослужит до 10 лет.
Также необходимо отметить, что матрасы на основе данного пружинного блока, обладают «эффектом волны». Из-за связанности пружин между собой, чувствуется движение партнера, то есть когда один человек переворачивается, встает с матраса или ложится на него, то «эффект «волны» передается и спящему рядом партнеру.
В каталоге матрасов и аксессуаров для сна производителя «АСАНА» вы можете купить недорогой матрас Lake на основе зависимого пружинного блока Боннель (Bonnell) с гарантией на 24 месяцев.
Пружинный блок — независимый, боннель, змейка. какой лучше? в каталоге Полезная информация 4hub
10/11/2020
Существует три вида пружинных блоков
- Независимый пружинный блок, он же ортопедический пружинный блок.
- Боннель, зависимый пружинный блок.
- Змейка пружинная.
У каждого блока есть свои плюсы и минусы, необходимо отталкиваться от основного назначения при выборе мягкой мебели.
- Независимый пружинный блок (НПБ)
Плюсы: НПБ уместен, если диван будет использоваться как кровать, для ежедневного сна. С ним вы сбережёте спину. НПБ упругий и комфортный. Блок принимает естественное положение спящего и тело находится в горизонтальном положение без эффекта гамака. Распределение нагрузки у блока локальное, каждый металлический виток пружины находится в индивидуальном нетканом чехле и практически не влияет на соседний виток. Данную особенность любят использовать в рекламе, ставя бокал с вином на матрас и прыгая рядом с ним. Бокал не разливается, потому что нету жёсткой зависимости между местом куда применили силу и там где стоит бокал.
Данную особенность любят использовать в рекламе, ставя бокал с вином на матрас и прыгая рядом с ним. Бокал не разливается, потому что нету жёсткой зависимости между местом куда применили силу и там где стоит бокал.
Минусы: независимый блок тяжелее остальных наполнителей. Стоимость выше на 4 — 7 т.р. чем диваны из альтернативных наполнителей.
Диваны с независимым пружинным блоком
- Боннель
Плюсы: по уровню комфорта, не уступает независимому пружинному блоку. По ощущению, когда садишься или ложишься, мягче независимого блока. На уровень мягкости влияет высота пружин, чем они выше, тем спальное место мягче, наиболее распространённая высота 100-120 мм.
Минусы: небольшой уровень шума, при сильном нажатии на сиденье до уровня каркаса. Происходит потому что пружины связаны между собой металлической проволокой из за трения метала слышен скрежет.
Дополнительно: у всех диванов с ПБ боннель можно изменить пружинные блоки на «независимые». Замена составит от 4 до 7 т.р. в зависимости от производителя.
Замена составит от 4 до 7 т.р. в зависимости от производителя.
Диваны с наполнением Боннель
- Змейка
Плюсы: недорогой и лёгкий тип пружинного блока. На диване с наполнением «змейка» удобно сидеть. Змейка крепится на деревянный или металлический каркас. Поверх змейки обязательно ставится пенополиуретан (ППУ) минимум 80 мм толщины, иначе змейка будет ощущаться.
Минусы: на данном ПБ неудобно спать из за эффекта «гамака». Центр масс образовывается посередине и позвоночник принимает неправильную форму.
Диваны с наполнением Змейка
Про пружинный блок на примере дивана Римини
=»video-container»>
Простое гармоническое движение: особое периодическое движение
Цели обучения
К концу этого раздела вы сможете:
- Опишите простой гармонический осциллятор.
- Объясните связь между простым гармоническим движением и волнами.

Колебания системы, в которой результирующая сила может быть описана законом Гука, имеют особое значение, поскольку они очень распространены. Это также простейшие колебательные системы. Простое гармоническое движение (SHM) — это название, данное колебательному движению для системы, в которой результирующая сила может быть описана законом Гука, и такая система называется простым гармоническим осциллятором . Если результирующая сила может быть описана законом Гука, а демпфирование (за счет трения или других неконсервативных сил) отсутствует, тогда простой гармонический осциллятор будет колебаться с одинаковым смещением по обе стороны от положения равновесия, как показано для объект на пружине на рисунке 1.Максимальное смещение от равновесия называется амплитудой X . Единицы измерения амплитуды и смещения одинаковы, но зависят от типа колебаний. Для объекта на пружине единицы измерения амплитуды и перемещения — метры; тогда как для звуковых колебаний у них есть единицы давления (а для других типов колебаний есть еще другие единицы). Поскольку амплитуда — это максимальное смещение, она связана с энергией колебаний.
Поскольку амплитуда — это максимальное смещение, она связана с энергией колебаний.
Рисунок 1.Предмет, прикрепленный к пружине, скользящей по поверхности без трения, представляет собой несложный простой гармонический осциллятор. При смещении из состояния равновесия объект совершает простое гармоническое движение с амплитудой X и периодом T . Максимальная скорость объекта достигается при прохождении через равновесие. Чем жестче пружина, тем меньше период T . Чем больше масса объекта, тем больше период T .
Эксперимент на вынос: SHM и мрамор
Найдите миску или таз, имеющий изнутри форму полусферы.Поместите мрамор внутрь чаши и периодически наклоняйте чашу, чтобы мрамор катился со дна чаши к одинаково высоким точкам по бокам чаши. Почувствуйте силу, необходимую для поддержания этого периодического движения. Что такое восстанавливающая сила и какую роль эта сила играет в простом гармоническом движении (SHM) мрамора?
Что такого значительного в простом гармоническом движении? Одна особенность заключается в том, что период T и частота f простого гармонического осциллятора не зависят от амплитуды. Струна гитары, например, будет колебаться с одной и той же частотой, независимо от того, мягко она или сильно нажата. Поскольку период постоянен, в качестве часов можно использовать простой гармонический осциллятор.
Струна гитары, например, будет колебаться с одной и той же частотой, независимо от того, мягко она или сильно нажата. Поскольку период постоянен, в качестве часов можно использовать простой гармонический осциллятор.
Два важных фактора действительно влияют на период простого гармонического осциллятора. Период связан с тем, насколько жесткая система. Очень жесткий объект имеет большую постоянную силы k , что приводит к тому, что система имеет меньший период. Например, вы можете отрегулировать жесткость трамплина — чем она жестче, тем быстрее она вибрирует и тем короче ее период.Период также зависит от массы колебательной системы. Чем массивнее система, тем больше период. Например, тяжелый человек на трамплине подпрыгивает вверх и вниз медленнее, чем легкий.
Фактически, масса m и силовая постоянная k являются всего лишь факторами , которые влияют на период и частоту простого гармонического движения.
Период простого гармонического осциллятора
Период простого гармонического осциллятора равен
.
[латекс] T = 2 \ pi \ sqrt {\ frac {m} {k}} \\ [/ latex]
и, поскольку [latex] f = \ frac {1} {T} \\ [/ latex], частота простого гармонического осциллятора равна
[латекс] f = \ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}} \\ [/ latex].
Обратите внимание, что ни T , ни f не зависят от амплитуды.
Эксперимент на вынос: колебания массы и линейки
Найдите две одинаковые деревянные или пластиковые линейки. Плотно прикрепите один конец каждой линейки к краю стола так, чтобы длина каждой линейки, выступающей из стола, была одинаковой. На свободный конец одной линейки прикрепите тяжелый предмет, например несколько крупных монет. Выщипывайте концы линейок одновременно и наблюдайте, какая из них претерпевает больше циклов за период времени, и измерьте период колебаний каждой из линейок.
Пример 1. Расчет частоты и периода колебаний: плохие амортизаторы в автомобиле
Если амортизаторы в автомобиле выходят из строя, то автомобиль будет раскачиваться при малейшей провокации, например, при наезде на неровности дороги и после остановки (см. Рисунок 2). Вычислите частоту и период этих колебаний для такого автомобиля, если масса автомобиля (включая его груз) составляет 900 кг, а постоянная силы ( k ) системы подвески составляет 6,53 × 10 4 Н / м.
Рисунок 2). Вычислите частоту и период этих колебаний для такого автомобиля, если масса автомобиля (включая его груз) составляет 900 кг, а постоянная силы ( k ) системы подвески составляет 6,53 × 10 4 Н / м.
Рис. 2. Подпрыгивающая машина совершает волнообразное движение. Если восстанавливающая сила в системе подвески может быть описана только законом Гука, тогда волна является синусоидальной функцией. (Волна — это след от фары при движении автомобиля вправо.)
Стратегия
Частота колебаний автомобиля будет соответствовать частоте простого гармонического осциллятора, как указано в уравнении [latex] f = \ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}} \\ [ /латекс]. Приведены как масса, так и силовая постоянная.{-1} = 1,36 \ text {Hz} \\ [/ latex]
Вы можете использовать [latex] T = 2 \ pi \ sqrt {\ frac {m} {k}} \\ [/ latex] для вычисления периода, но проще использовать соотношение [latex] T = \ frac {1} {f} \\ [/ latex] и замените только что найденное значение на f :
[латекс] \ displaystyle {T} = \ frac {1} {f} = \ frac {1} {1. 356 \ text {Hz}} = 0,738 \ text {s} \\ [/ latex]
356 \ text {Hz}} = 0,738 \ text {s} \\ [/ latex]
Обсуждение
Значения T и f кажутся подходящими для подпрыгивающего автомобиля. Вы можете наблюдать эти колебания, если сильно надавите на конец автомобиля и отпустите.
Связь между простым гармоническим движением и волнами
Рис. 3. Вертикальное положение объекта, подпрыгивающего на пружине, записывается на полоске движущейся бумаги, оставляя синусоидальную волну.
Если бы была сделана фотография прыгающего автомобиля с выдержкой времени, когда он проезжал мимо, фара образовала бы волнообразную полосу, как показано на рисунке 2. Точно так же на рисунке 3 показан объект, подпрыгивающий на пружине, оставляющий волнообразный «след». своего положения на движущейся полосе бумаги. Обе волны являются синусоидальными функциями.Все простые гармонические движения тесно связаны с синусоидальными и косинусоидальными волнами.
Смещение как функция времени t при любом простом гармоническом движении, то есть таком, в котором результирующая восстанавливающая сила может быть описана законом Гука, определяется как
[латекс] x (t) = X \ cos \ frac {2 \ pi {t}} {T} \\ [/ latex],
, где X — амплитуда. При t = 0 начальное положение составляет x 0 = X , а смещение колеблется назад и вперед с периодом T . (Когда t = T , мы снова получаем x = X , потому что cos 2π = 1.). Кроме того, из этого выражения для x , скорость v как функция времени определяется как
При t = 0 начальное положение составляет x 0 = X , а смещение колеблется назад и вперед с периодом T . (Когда t = T , мы снова получаем x = X , потому что cos 2π = 1.). Кроме того, из этого выражения для x , скорость v как функция времени определяется как
[латекс] v (t) = — v _ {\ text {max}} \ sin \ left (\ frac {2 \ pi {t}} {T} \ right) \\ [/ latex], где [латекс] v _ {\ text {max}} = \ frac {2 \ pi {X}} {T} = X \ sqrt {\ frac {k} {m}} \\ [/ latex].
Объект имеет нулевую скорость при максимальном смещении — например, v = 0, когда t = 0, и в это время x = X .Знак минус в первом уравнении для v ( t ) указывает правильное направление скорости. Например, сразу после начала движения скорость отрицательна, потому что система движется обратно к точке равновесия. Наконец, мы можем получить выражение для ускорения, используя второй закон Ньютона. [Тогда у нас есть x ( t ), v ( t ), t и a ( t ), величины, необходимые для кинематики и описания простого гармонического движения.] Согласно второму закону Ньютона, ускорение составляет [латекс] a = \ frac {F} {m} = \ frac {kx} {m} \\ [/ latex] . Итак, a ( t ) также является функцией косинуса:
[Тогда у нас есть x ( t ), v ( t ), t и a ( t ), величины, необходимые для кинематики и описания простого гармонического движения.] Согласно второму закону Ньютона, ускорение составляет [латекс] a = \ frac {F} {m} = \ frac {kx} {m} \\ [/ latex] . Итак, a ( t ) также является функцией косинуса:
[латекс] a (t) = — \ frac {kX} {m} \ cos \ frac {2 \ pi {t}} {T} \\ [/ latex].
Следовательно, a ( t ) прямо пропорционально и в противоположном направлении к a ( t ).
На рисунке 4 показано простое гармоническое движение объекта на пружине и представлены графики x ( t ), v ( t ) и a ( t ) в зависимости от времени.
Рис. 4. Графики зависимости t от движения объекта на пружине. Суммарная сила, действующая на объект, может быть описана законом Гука, поэтому объект совершает простое гармоническое движение. Обратите внимание, что исходное положение имеет максимальное значение вертикального смещения X ; v изначально равно нулю, а затем отрицательно по мере движения объекта; и начальное ускорение отрицательное, возвращается к положению равновесия и становится нулевым в этой точке.
Обратите внимание, что исходное положение имеет максимальное значение вертикального смещения X ; v изначально равно нулю, а затем отрицательно по мере движения объекта; и начальное ускорение отрицательное, возвращается к положению равновесия и становится нулевым в этой точке.
Наиболее важным моментом здесь является то, что эти уравнения математически просты и справедливы для всех простых гармонических движений.Они очень полезны при визуализации волн, связанных с простым гармоническим движением, включая визуализацию того, как волны складываются друг с другом.
Проверьте свое понимание
Часть 1
Предположим, вы взяли струну банджо. Вы слышите одну ноту, которая начинается вслух и постепенно затихает. Опишите, что происходит со звуковыми волнами с точки зрения периода, частоты и амплитуды по мере уменьшения громкости звука.
Решение
Частота и период практически не изменились.При уменьшении громкости уменьшается только амплитуда.
Часть 2
Няня толкает ребенка на качелях. В точке, где качание достигает x , где будет расположена соответствующая точка на волне этого движения?
Решение
x — максимальная деформация, соответствующая амплитуде волны. Точка на волне будет либо на самом верху, либо на самом низу кривой.
Исследования PhET: массы и пружины
Реалистичная лаборатория масс и пружин.Подвесьте массы к пружинам и отрегулируйте жесткость и демпфирование пружины. Вы даже можете замедлить время. Перенесите лабораторию на разные планеты. На диаграмме показана кинетическая, потенциальная и тепловая энергия каждой пружины.
Щелкните, чтобы запустить моделирование.
Избранные решения
- Простое гармоническое движение — это колебательное движение для системы, которое можно описать только законом Гука. Такую систему еще называют простым гармоническим осциллятором.
- Максимальное смещение — это амплитуда X .
 Период T и частота f простого гармонического осциллятора задаются выражениями [latex] T = 2 \ pi \ sqrt {\ frac {m} {k}} \\ [/ latex] и [latex] f = \ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}} \\ [/ latex], где м — масса системы.
Период T и частота f простого гармонического осциллятора задаются выражениями [latex] T = 2 \ pi \ sqrt {\ frac {m} {k}} \\ [/ latex] и [latex] f = \ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}} \\ [/ latex], где м — масса системы. - Смещение при простом гармоническом движении как функция времени определяется как [latex] x \ left (t \ right) = X \ text {cos} \ frac {2 \ pi {t}} {T} \\ [/ latex ].
- Скорость определяется как [латекс] v \ left (t \ right) = — {v} _ {\ text {max}} \ text {sin} \ frac {2 \ pi {t}} {T} \\ [/ latex], где [latex] {v} _ {\ text {max}} = \ sqrt {\ frac {k} {m}} X \\ [/ latex].
- Ускорение составляет [латекс] a (t) = — \ frac {kX} {m} \ cos \ frac {2 \ pi {t}} {T} \\ [/ latex].
Концептуальные вопросы
- Какие условия должны быть выполнены для создания простого гармонического движения?
- (a) Если частота для некоторого колебания непостоянна, может ли колебание быть простым гармоническим движением? б) Можете ли вы привести примеры гармонического движения, в котором частота может зависеть от амплитуды?
- Приведите пример простого гармонического осциллятора, особо отметив, что его частота не зависит от амплитуды.

- Объясните, почему вы ожидаете, что объект, сделанный из жесткого материала, будет вибрировать с большей частотой, чем аналогичный объект, сделанный из губчатого материала.
- Когда вы проезжаете грузовой автомобиль с прицепом по шоссе, вы замечаете, что его прицеп медленно подпрыгивает вверх и вниз. Более вероятно, что прицеп сильно загружен или почти пустой? Поясните свой ответ.
- Некоторые люди модифицируют автомобили, чтобы они были намного ближе к земле, чем когда они были изготовлены. Стоит ли устанавливать более жесткие пружины? Поясните свой ответ.
Задачи и упражнения
- Часы с кукушкой следят за временем, заставляя массу подпрыгивать на пружине, обычно что-то милое, вроде херувима в кресле. Какая силовая постоянная необходима для получения периода 0,500 с для массы 0,0150 кг?
- Если жесткость пружины простого гармонического осциллятора удвоится, на какой коэффициент нужно изменить массу системы, чтобы частота движения оставалась прежней?
- Груз весом 0,500 кг, подвешенный на пружине, колеблется с периодом 1.
 50 с. Какую массу нужно добавить к объекту, чтобы изменить период до 2,00 с?
50 с. Какую массу нужно добавить к объекту, чтобы изменить период до 2,00 с? - Насколько проста в выборе массы объекта (как в процентах, так и по массе) в предыдущей задаче, если вы не хотите, чтобы новый период был больше 2,01 с или меньше 1,99 с?
- Предположим, вы прикрепляете объект массой м к вертикальной пружине, первоначально находящейся в состоянии покоя, и позволяете ему подпрыгивать вверх и вниз. Вы высвобождаете объект из состояния покоя на исходной длине упора пружины.(а) Покажите, что пружина оказывает на объект восходящую силу 2,00 мг в его самой нижней точке. (b) Если пружина имеет силовую постоянную 10,0 Н / м и объект массой 0,25 кг приводится в движение, как описано, найдите амплитуду колебаний. (c) Найдите максимальную скорость.
- Дайвер на трамплине совершает простое гармоническое движение. Ее масса 55,0 кг, период движения 0,800 с. Следующий дайвер — мужчина, период простых гармонических колебаний которого составляет 1,05 с. Какова его масса, если масса доски ничтожна?
- Предположим, что доска для прыжков в воду, на которой никого нет, подпрыгивает вверх и вниз, совершая простое гармоническое движение с частотой 4.
 00 Гц. Доска имеет полезную массу 10,0 кг. Какова частота простого гармонического движения дайвера весом 75,0 кг на доске?
00 Гц. Доска имеет полезную массу 10,0 кг. Какова частота простого гармонического движения дайвера весом 75,0 кг на доске? - Устройство, изображенное на рис. 6, развлекает младенцев, удерживая их от блужданий. Ребенок подпрыгивает в привязи, подвешенной к дверной коробке с помощью пружины.
Рис. 6. В этой детской игрушке используются пружины, чтобы развлекать младенцев. (Источник: Humboldthead, Flickr)
(a) Если пружина растягивается на 0,250 м, поддерживая 8.Ребенок 0 кг, какова его постоянная пружины? б) Сколько времени на один полный прыжок этого ребенка? (c) Какова максимальная скорость ребенка, если амплитуда его прыжка составляет 0,200 м?
- Парашютист весом 90,0 кг, подвешенный на парашюте, подпрыгивает вверх и вниз с периодом 1,50 с. Каков новый период колебаний, когда второй парашютист массой 60,0 кг свисает с ног первого, как показано на рисунке 7.
Рис. 7. На колебания одного парашютиста вот-вот повлияет второй парашютист.(Источник: армия США, www.
 army.mil)
army.mil)
Глоссарий
амплитуда : максимальное смещение от положения равновесия объекта, колеблющегося вокруг положения равновесия
простое гармоническое движение: колебательное движение в системе, где результирующая сила может быть описана законом Гука
простой гармонический осциллятор: устройство, реализующее закон Гука, такое как масса, прикрепленная к пружине, при этом другой конец пружины соединен с жесткой опорой, такой как стена
Избранные решения проблем и упражнения
1.2,37 Н / м
3. 0,389 кг
6. 94,7 кг
9. 1.94 с
15. КОЛЕБАНИЯ
15. КОЛЕБАНИЯ
Любое движение, которое повторяется через равные промежутки времени, называется гармоникой .
Движение . Частица совершает движение по простой гармонике , если ее
смещение от начала координат как функция времени определяется как
где x m , [omega] и [phi] — константы, не зависящие от
время. Величина x м называется амплитудой
Величина x м называется амплитудой
движение и является максимальным смещением массы. Изменяющийся во времени
величина ([omega] t + [phi]) называется фазой движения
а [phi] называется фазовой постоянной . Фазовая постоянная равна
определяется начальными условиями. Угловая частота
[омега] является характеристикой системы и не зависит от начального
условия. Единица угловой частоты — рад / с.В
период Т движения определяется как время, необходимое для
совершить одно колебание. Следовательно, смещение x (t) должно вернуться к своему
начальное значение через один период
x (t) = x (t + T)
Это эквивалентно
Используя соотношение
сразу видно, что
Количество колебаний, совершаемых за секунду, называется
частота колебаний .Обозначение частоты — [ню].
и его единицей является Герц (Гц):
1 Гц = 1 колебание в секунду = 1 с -1
Период T и частота [nu] связаны следующим образом:
Скорость объекта, совершающего простое гармоническое движение, может быть
легко рассчитывается
Положительная величина [омега] x м называется
амплитуда скорости и является максимальной скоростью объекта.Обратите внимание, что фазы скорости и смещения отличаются на 90 градусов. Это
означает, что скорость максимальна, когда смещение равно нулю, и наоборот.
наоборот . Ускорение объекта, совершающего простое гармоническое движение.
выдается
Положительная величина [омега] 2 x м — это
амплитуда ускорения a м . Используя выражение для
x (t) выражение для a (t) можно переписать как
Это показывает, что ускорение пропорционально смещению,
но противоположный по знаку.Силу, действующую на массу, можно рассчитать с помощью
Второй закон Ньютона
Это уравнение силы аналогично силе пружины.
(Закон Гука)
F = — k x
Сравнивая эти последние два уравнения, мы заключаем, что
k = m [omega] 2
и
« Простое гармоническое движение — это движение, совершаемое частицей
масса m, подверженная действию силы F, пропорциональной перемещению
частица, но противоположная по знаку. «
Система, показанная на рисунке 15.1, образует простой гармонический осциллятор. Так и будет
колебаться с угловой частотой [омега], задаваемой
Период колебаний T равен
.
Полная механическая энергия простого гармонического осциллятора состоит из
потенциальной и кинетической энергии. Потенциальная энергия системы задана
по
Рисунок 15.1. Простой гармонический осциллятор.
Кинетическая энергия системы определяется как
.
Теперь можно рассчитать полную механическую энергию системы
Полная механическая энергия простого гармонического осциллятора равна
константа (не зависит от времени). Однако кинетический и потенциальный
энергии — это функции времени.
Пример: крутильный маятник
Работа торсионного маятника связана с закручиванием
подвесной трос.Движение, описываемое торсионным маятником, называется
угловое простое гармоническое движение . Восстанавливающий момент равен
.
где [каппа] — постоянная, зависящая от свойств
подвесной трос (его длина, диаметр и материал). Для заданного крутящего момента мы можем
рассчитать угловое ускорение a
или
Сравнивая это уравнение с соотношением линейных
ускорение и линейное перемещение объекта, заключаем, что
Период торсионного маятника равен
.
Пример: классический простой маятник
Классический простой маятник показан на рисунке 15.2. Он состоит
из массы m, подвешенной на безмассовой струне длиной L. Силы
на массу действуют гравитационная сила m g и натяжение T в
нить. Радиальная составляющая гравитационной силы, m g cos ([theta]),
определяет натяжение проволоки, но не изменяет движение массы.
Тангенциальная составляющая гравитационной силы, m g sin ([theta]), равна
всегда направлен в сторону покоя маятника. Этот компонент
гравитационная сила называется возвращающей силой:
Для малых углов sin ([theta]) ~ [theta].Это показывает, что
где s — перемещение массы по дуге. Снова мы
сделать вывод, что возвращающая сила пропорциональна смещению, и
противоположного знака . Следовательно, движение — это движение гармонического осциллятора.
Ускорение массы связано с перемещением s
Рисунок 15.2. Классический простой маятник.
Это сразу указывает на то, что задана угловая частота [омега]
по
и, следовательно, период движения равен
Рисунок 15.3. Физический маятник.
Пример: физический маятник
В реальном мире с маятниками все далеко не так просто. В общем, масса
маятник не сосредоточен в одной точке, а будет распределен.
На рисунке 15.3 показан физический маятник. Физический маятник приостановлен
через точку О. Действие силы тяжести можно заменить
действие единственной силы величиной m g, действующей на центр
гравитация маятника (который равен центру масс, если
ускорение свободного падения постоянно).Результирующий крутящий момент (относительно
к O) дается
где h — расстояние между осью вращения и центром
сила тяжести. В пределе малых углов этот крутящий момент можно переписать как
Угловое ускорение маятника a связано с крутящим моментом
[tau] и инерция вращения I
Таким образом, мы заключаем, что
Это снова уравнение гармонического движения с угловым
частота по
и период равный
Обратите внимание, что простой маятник — это частный случай физического
маятник: h = L и I = m L 2 .Период колебаний равен
затем присвоено
Примечание : Уравнения движения, описывающие гармоническое движение, все
имеют следующий вид:
Общее решение этого дифференциального уравнения:
Это легко показать, дважды дифференцируя x (t) по
время
и
Простое гармоническое движение — это частный случай, когда амплитуды A
и B равны.В этом случае x (t) можно переписать как
Это уравнение описывает простое гармоническое движение с угловым
частота равна [омега].
Пример: проблема 33P
Две пружины прикреплены к блоку массой m и к неподвижному
поддерживает, как показано на рисунке 15.4. Покажите, что частота колебаний на
поверхность без трения —
Рисунок 15.4. Задача 33П.
Когда пружина 1 растягивается на x, пружина 2 сжимается тем же
расстояние. Полная сила, действующая на массу, представляет собой сумму прилагаемых сил.
этими двумя источниками. Обратите внимание, что обе силы всегда указывают на одно и то же.
направление.
Это похоже на уравнение движения простой гармоники
осциллятор. Это уравнение можно переписать как
или
Мы заключаем, что угловая частота равна
а период T на
Пример: Задача 35P
Две пружины соединены и соединены массой m, как показано на
Рисунок 15.5. Поверхности без трения. Если каждая пружина имеет силу
константа k, покажите, что частота колебаний m равна
Рисунок 15.5. Задача 35П
Предположим, что пружинные постоянные не совпадают. Поскольку масса
колеблется, пружина 1 растягивается или сжимается на расстояние x 1 ;
соответствующее расстояние для другой пружины называется x 2 . От
Согласно третьему закону Ньютона силы, действующие друг на друга пружинами, равны
по величине, но направлены в противоположные стороны.Сила пружины 1
весной 2 выдается
Это уравнение означает, что если пружина 1 растянута (x 1 >
0) сила, прилагаемая пружиной 1 к пружине 2, имеет отрицательное значение.
направление. Усилие, прилагаемое пружиной 2 к пружине 1, равно
.
Это уравнение означает, что если пружина 2 растянута (x 2 >
0) сила, прилагаемая пружиной 2 к пружине 1, указана в положительном
направление.Применяя третий закон Ньютона, заключаем, что
Смещение самой массы равно
.
и, следовательно,
F 1 — единственная сила, действующая на массу, а F 1
равно k 1 x 1 . Теперь можно использовать предыдущее соотношение
для выражения силы F 1 через смещение x:
Мы заключаем, что две пружины с жесткостью пружины k 1 и
k 2 и соедините, как показано на рисунке 15.5, действовать как сингл
пружина с жесткостью пружины k, где k равно
До сих пор мы обсуждали системы, в которых сила пропорциональна
к смещению, но указал в противоположном направлении. В этих случаях
движение системы можно описать простым гармоническим движением. Однако если
включив силу трения, движение больше не будет простым гармоническим.
Система по-прежнему будет колебаться, но ее амплитуда будет медленно уменьшаться в течение
время.
Предположим, что общая сила, действующая на массу, не только пропорциональна
его смещение, но также и его скорость. Суммарная сила может быть представлена
следующим образом
В этой формуле b называется постоянной демпфирования .
Подставляя выражение для силы через ускорение, мы
получить следующее дифференциальное уравнение
Общее решение этого дифференциального уравнения будет иметь вид
Подставляя это выражение в дифференциальное уравнение, получаем
Это уравнение можно переписать как
и решения для [omega]:
Подставляя это в выражение для x (t), получаем
Мы видим, что амплитуда движения постепенно уменьшается со временем.Это также верно для кинетической энергии осциллятора. В любой момент
механическую энергию осциллятора можно рассчитать, используя выражение для
х (т):
Пример: проблема 87P
Генератор затухающих гармоник включает в себя блок (m = 2 кг),
пружина (k = 10 Н / м) и демпфирующая сила F = — b v. Сначала она колеблется
амплитудой 0,25 м; из-за затухания амплитуда падает до
три четверти от первоначального значения после четырех полных циклов.а) Что такое
значение b? (б). Сколько энергии теряется за эти четыре цикла?
Зависимость амплитуды колебаний от времени определяется выражением
.
Период одного колебания равен
.
Следовательно, амплитуда после 4 колебаний равна
.
Угловая частота [омега] связана с жесткостью пружины k и
масса m следующим образом
Используя это выражение, получаем для b
Механическая энергия, теряемая во время этих 4 колебаний, также может быть уменьшена.
легко рассчитывается
Случай гармонического осциллятора, управляемого синусоидальной переменной силой
чрезвычайно важен во многих областях физики.В предыдущем
в разделах мы обсудили несколько примеров гармонических осцилляторов, а для
Каждой системе мы смогли рассчитать собственную частоту
[omega] 0 , (например, для пружины
[омега] 0 2 = к / м). Уравнение движения для
осциллятор, на котором не действует демпфирующая сила и внешняя сила
подано по
Предположим, что к этой системе приложена внешняя сила F (t).Внешний
сила имеет амплитуду m F 0 и угловую частоту [омега]. В
уравнение движения, описывающее систему, теперь дается
Устойчивое состояние (состояние системы после любого
переходные эффекты поутихли) срабатывание системы будет точно на
частота возбуждения. В противном случае относительная фаза между силой и ответом
со временем изменится. Таким образом, установившийся отклик гармоники
осциллятор находится на управляющей частоте [омега], а не на
собственная частота [омега] 0 .
Общее решение уравнения движения:
Подставляя это выражение в уравнение движения, получаем
Это уравнение можно переписать с помощью некоторых тригонометрических соотношений
Это уравнение может быть выполнено только в том случае, если коэффициенты при
cos ([omega] t) и sin ([omega] t) равны нулю.Это означает, что
и
Обычно A! = 0 и [omega]! = [Omega] 0 . Первое
условие, чем показывает, что
Второе условие теперь можно переписать как
.
Амплитуда гармонического осциллятора равна
.
Амплитуда колебаний системы становится очень большой, если
[омега] приближается к [омега] 0 .Система называется в
резонанс , когда это произойдет.
Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса.
1. Введение в Spring Framework
Строительные блоки, описанные ранее, делают Spring логичным
выбор во многих сценариях, от апплетов до полноценного предприятия
приложения, использующие функции управления транзакциями Spring и
интеграция с веб-фреймворком.
Весна декларативная
функции управления транзакциями делают веб-приложение полностью
транзакционный, как если бы вы использовали управляемый контейнером EJB
сделки. Вся ваша индивидуальная бизнес-логика может быть реализована с помощью
простые POJO и управляются контейнером Spring IoC. Дополнительные услуги
включать поддержку отправки электронной почты и проверки, не зависящей от
веб-слой, который позволяет вам выбирать, где выполнять правила проверки.
Поддержка ORM Spring интегрирована с JPA, Hibernate, JDO и iBatis;
например, при использовании Hibernate вы можете продолжать использовать существующий
файлы сопоставления и стандартный Hibernate
SessionFactory конфигурация.Форма
контроллеры легко интегрируют веб-уровень с моделью предметной области,
устранение необходимости в ActionForms или других классах
которые преобразуют параметры HTTP в значения для вашей модели предметной области.
Иногда обстоятельства не позволяют полностью перейти на
разные рамки. Spring Framework делает , а не
заставляют вас использовать все, что в нем есть; это не
решение «все или ничего» . Созданы существующие интерфейсы
с WebWork, Struts, Tapestry или другими фреймворками пользовательского интерфейса могут быть интегрированы
со средним уровнем на основе Spring, который позволяет использовать Spring
особенности сделки.Вам просто нужно подключить свою бизнес-логику, используя
ApplicationContext и используйте
WebApplicationContext для интеграции в вашу сеть
слой.
Если вам нужно получить доступ к существующему коду через веб-службы, вы можете
используйте Spring’s Hessian- , Burlap- ,
Rmi- или JaxRpcProxyFactory
классы. Включение удаленного доступа к существующим приложениям не
трудный.
Spring Framework также предоставляет доступ и
уровень абстракции для Enterprise JavaBeans, позволяющий повторно использовать
ваши существующие POJO и оберните их в сессионные bean-компоненты без сохранения состояния для использования в
масштабируемые, отказоустойчивые веб-приложения, которым могут потребоваться декларативные
безопасность.
1.3.1 Соглашения об управлении зависимостями и присвоении имен
Управление зависимостями и внедрение зависимостей отличаются
вещи. Чтобы добавить в свое приложение эти приятные функции Spring (например,
внедрение зависимостей) вам необходимо собрать все необходимые библиотеки (jar
files) и поместите их в путь к классам во время выполнения и, возможно, в
время компиляции. Эти зависимости не являются виртуальными компонентами, которые
внедренные, но физические ресурсы в файловой системе (обычно). В
процесс управления зависимостями включает в себя определение местоположения этих ресурсов,
сохраняя их и добавляя в пути к классам.Зависимости могут быть прямыми
(например, мое приложение зависит от Spring во время выполнения) или косвенно (например, мой
приложение зависит от commons-dbcp , который зависит от
общий бассейн ). Косвенные зависимости также известны как
«транзитивные», и именно те зависимости труднее всего идентифицировать
и управлять.
Если вы собираетесь использовать Spring, вам нужно получить копию jar
библиотеки, которые содержат части Spring, которые вам нужны. Чтобы сделать это
проще Spring упакован как набор модулей, которые разделяют
как можно больше зависимостей, поэтому, например, если вы не хотите
напишите веб-приложение, в котором вам не нужны модули Spring-Web.Ссылаться
для модулей библиотеки Spring в этом руководстве мы используем сокращенное именование
условное обозначение пружина- * или пружина - *. jar, где «*»
представляет собой краткое название модуля (например, пружинный сердечник ,
Spring-WebMVC , Spring-JMS и т. Д.). Настоящий
имя файла jar, которое вы используете, может быть в этой форме (см. ниже) или может
нет, и обычно он также имеет номер версии в имени файла (например,
spring-core-3.0.0.RELEASE.jar ).
В целом Spring публикует свои артефакты в четырех разных
места:
На сайте сообщества для скачивания http: // www.springsource.org/download/community.
Здесь вы найдете все баночки Spring, объединенные в zip-файл.
для легкой загрузки. Названия банок здесь начиная с версии 3.0
находятся в форме
org.springframework. * - <версия> .jar.Maven Central, репозиторий по умолчанию, который Maven
запросы и не требует специальной настройки для использования.
Многие из общих библиотек, от которых зависит Spring, также
доступно в Maven Central и в большой части Spring
сообщество использует Maven для управления зависимостями, так что это
им удобно.Названия банок здесь в виде
spring - * -и идентификатор группы Maven.jar
орг. Пружинный каркас.Репозиторий корпоративных пакетов (EBR), которым управляет
SpringSource, а также содержит все библиотеки, которые интегрируются с
Весна. Репозитории Maven и Ivy доступны здесь для всех.
Spring jar-файлы и их зависимости, а также большое количество других
общие библиотеки, которые люди используют в приложениях с Spring. Оба
полные выпуски, а также вехи и моментальные снимки разработки
развернут здесь.Имена файлов jar имеют ту же форму, что и
сообщество скачать
(org.springframework. * -), а.jar
зависимости также в этой «длинной» форме, с внешними библиотеками
(не из SpringSource) с префиксом
com.springsource. См. FAQ
для дополнительной информации.В общедоступном репозитории Maven, размещенном на Amazon S3 для
снимки состояния разработки и контрольные выпуски (копия финального
релизы тоже проходят здесь). Имена файлов jar совпадают
как Maven Central, так что это полезное место для получения
разрабатываемые версии Spring для использования с другими развернутыми библиотеками
в Maven Central.
Итак, первое, что вам нужно решить, это как управлять своим
зависимости: большинство людей используют автоматизированные системы, такие как Maven или Ivy, но
вы также можете сделать это вручную, загрузив все банки самостоятельно. Когда
Получив Spring с Maven или Ivy, вы должны решить, в каком месте
вы получите это от. В общем, если вам небезразлична OSGi, используйте EBR,
поскольку в нем хранятся совместимые с OSGi артефакты для всех Spring
зависимости, такие как Hibernate и Freemarker. Если OSGi не имеет значения
вам, любое место работает, хотя есть некоторые плюсы и минусы между
их.В общем, выберите для своего проекта то или иное место; не
смешайте их. Это особенно важно, поскольку артефакты EBR обязательно
используйте другое соглашение об именах, чем артефакты Maven Central.
Таблица 1.1. Сравнение Maven Central и SpringSource EBR
Репозитории
| Функция | Maven Central | EBR | |
|---|---|---|---|
| OSGi-совместим | Неявно | Да | |
| 912 тысяч артефактов все виды | Сот; те, которые Spring интегрирует с | ||
| Согласованными соглашениями об именах | Нет | Да | |
| Соглашение об именах: GroupId | Различается.В более новых артефактах часто используется доменное имя, например org.slf4j. Более старые часто используют просто имя артефакта, например log4j. | Доменное имя источника или корень основного пакета, например org.springframework | |
| Соглашение об именах: ArtifactId | Различается. Обычно имя проекта или модуля с использованием разделитель дефис «-«, например пружинный сердечник, logj4. | Символическое имя пакета, производное от основного пакета корень, например org.springframework.beans. Если бы банку пришлось исправлен для обеспечения соответствия OSGi, затем com.источник добавлено, например com.springsource.org.apache.log4j | |
| Соглашение об именах: Версия | Различается. Многие новые артефакты используют m.m.m или m.m.m.X (с m = цифра, X = текст). Старшие используют m.m. Некоторые тоже. Заказ определяется, но не часто используется, поэтому не строго надежный. | Номер версии OSGi m.m.m.X, например 3.0.0.RC3. Текст квалификатор накладывает алфавитный порядок на версии с те же числовые значения. | |
| Публикация | Обычно автоматически через rsync или обновления системы контроля версий.Авторы проекта могут загружать отдельные jar-файлы в JIRA. | Руководство (JIRA обрабатывается SpringSource) | |
| Контроль качества | В соответствии с политикой. Ответственность за точность несет авторы. | Extensive для манифеста OSGi, Maven POM и Ivy метаданные. Контроль качества выполняется командой Spring. | |
| Хостинг | Contegix. Финансируется Sonatype с несколькими зеркала. | S3 финансируется SpringSource. | |
| Утилиты поиска | Разные | http: // www.springsource.com/repository | |
| Интеграция с инструментами SpringSource | Интеграция через STS с зависимостью Maven управление | Обширная интеграция через STS с Maven, Roo, CloudFoundry |
Зависимости пружины и зависимости от пружины
Хотя Spring обеспечивает интеграцию и поддержку огромного
набор корпоративных и других внешних инструментов, он намеренно сохраняет
его обязательные зависимости до абсолютного минимума: у вас не должно быть
найти и загрузить (даже автоматически) большое количество jar
библиотеки, чтобы использовать Spring для простых случаев использования.Для базового
внедрение зависимости есть только одна обязательная внешняя зависимость,
и это для ведения журнала (см. ниже более подробное описание
параметры ведения журнала).
Далее мы опишем основные шаги, необходимые для настройки
приложение, которое зависит от Spring, сначала с Maven, а затем с
Айви. Во всех случаях, если что-то неясно, обратитесь к документации.
вашей системы управления зависимостями или посмотрите пример кода —
Сама Spring использует Ivy для управления зависимостями при построении, и
наши образцы в основном используют Maven.
Управление зависимостями Maven
Если вы используете Maven для управления зависимостями, вы даже не
необходимо явно указать зависимость ведения журнала. Например, чтобы
создать контекст приложения и использовать внедрение зависимостей для
настроить приложение, ваши зависимости Maven будут выглядеть как
это:
<зависимости>
<зависимость>
org.springframework
весенний контекст
<версия> 3.0.0.RELEASE
время выполнения
Вот и все. Обратите внимание, что область действия может быть объявлена как среда выполнения, если вы
не нужно компилировать с API Spring, что обычно бывает
для основных случаев использования внедрения зависимостей.
В примере мы использовали соглашения об именах Maven Central.
выше, так что это работает с Maven Central или SpringSource S3 Maven
репозиторий. Чтобы использовать репозиторий S3 Maven (например, для вех или
снимки разработчика) необходимо указать расположение репозитория в
ваша конфигурация Maven.Для полных релизов:
<хранилища>
<репозиторий>
com.springsource.repository.maven.release
http://repo.springsource.org/release/
false Для вех:
<хранилища>
<репозиторий>
com.springsource.repository.maven.milestone
http: // репо.springsource.org/milestone/
false А для снимков:
<хранилища>
<репозиторий>
com.springsource.repository.maven.snapshot
http://repo.springsource.org/snapshot/
true Чтобы использовать SpringSource EBR, вам потребуется другой
соглашение об именах для зависимостей.Имена обычно легко
угадайте, например в данном случае это:
<зависимости>
<зависимость>
org.springframework
org.springframework.context
3.0.0.RELEASE
время выполнения
Также необходимо указать местонахождение репозитория
явно (важен только URL):
<хранилища>
<репозиторий>
com.springsource.repository.bundles.release
http://repository.springsource.com/maven/bundles/release/
Если вы управляете своими зависимостями вручную, URL-адрес в
объявление репозитория выше недоступно для просмотра, но есть пользователь
интерфейс на http://www.springsource.com/repository
который можно использовать для поиска и загрузки зависимостей. Он также имеет
удобные фрагменты конфигурации Maven и Ivy, которые вы можете скопировать и
вставьте, если вы используете эти инструменты.
Управление зависимостями плюща
Если вы предпочитаете использовать Ivy для управления зависимостями
тогда есть похожие названия и варианты конфигурации.
Чтобы настроить Ivy так, чтобы он указывал на SpringSource EBR, добавьте
следующие резолверы на ваш
ivysettings.xml :
<решатели>
XML-код выше недействителен, потому что строки слишком длинные — если
вы копируете и вставляете, а затем удаляете лишние окончания строк в середине
шаблоны URL.
После того, как Ivy настроен на просмотр EBR, добавляется зависимость.
легкий. Просто откройте страницу сведений о рассматриваемом пакете в
браузер репозитория, и вы найдете готовый фрагмент Ivy, чтобы
включить в свой раздел зависимостей. Например (в
ivy.xml ):
Ведение журнала — очень важная зависимость для Spring, потому что а) это
единственная обязательная внешняя зависимость, б) всем нравится видеть некоторые
вывод из инструментов, которые они используют, и c) Spring интегрируется с множеством
других инструментов, все из которых также выбрали ведение журнала
зависимость. Одна из целей разработчика приложения часто состоит в том, чтобы
настроили единое ведение журнала в центральном месте для всего
приложение, включая все внешние компоненты.Это сложнее
чем это могло бы быть, поскольку существует так много вариантов ведения журнала
фреймворк.
Обязательной зависимостью ведения журнала в Spring является Jakarta Commons.
Logging API (JCL). Мы компилируем с JCL, а также делаем JCL
Журнал объектов, видимых для классов, расширяющих
Spring Framework. Для пользователей важно, чтобы все версии Spring
использовать ту же библиотеку журналов: миграция проста, потому что в обратном направлении
совместимость сохраняется даже с приложениями, расширяющими Spring.Мы делаем это так, чтобы один из модулей Spring зависел от
явно на commons-logging (каноническая реализация
из JCL), а затем сделать все остальные модули зависимыми от этого при компиляции
время. Если вы, например, используете Maven и хотите знать, где вы выбрали
вверх по зависимости от commons-logging , то это от
Spring и, в частности, из центрального модуля, называемого
пружинный стержень .
Самое приятное в , зарегистрированном в общем журнале , заключается в том, что вы
больше ничего не нужно, чтобы ваше приложение работало.Имеет время выполнения
алгоритм обнаружения, который ищет другие структуры каротажа в хорошо
известные места в пути к классам и использует то, которое считает подходящим
(или вы можете сказать, какой из них, если вам нужно). Если больше ничего нет
доступно, вы получаете довольно красивые журналы только из JDK
(java.util.logging или JUL для краткости). Вы должны обнаружить, что ваша весна
приложение работает и успешно записывается в консоль из коробки в большинстве
ситуации, и это важно.
Не используется ведение журнала Commons
К сожалению, алгоритм обнаружения времени выполнения в
commons-logging , хотя и удобен для конечного пользователя, но
проблематично.Если бы мы могли повернуть время вспять и начать весну сейчас
в качестве нового проекта он будет использовать другую зависимость от ведения журнала. В
первым выбором, вероятно, будет Simple Logging Facade для Java (SLF4J), который также используется многими
других инструментов, которые люди используют со Spring внутри своих
Приложения.
Отключить commons-logging легко: просто сделайте
убедитесь, что его нет в пути к классам во время выполнения. В терминах Maven вы исключаете
зависимости и из-за того, как зависимости Spring
объявлены, вам нужно сделать это только один раз.
<зависимости>
<зависимость>
org.springframework
весенний контекст
3.0.0.RELEASE
время выполнения
<исключения>
<исключение>
commons-logging
общедоступное ведение журнала
Теперь это приложение, вероятно, не работает, потому что нет
реализация JCL API в пути к классам, чтобы исправить его новым
должен быть предоставлен.В следующем разделе мы покажем вам, как предоставить
альтернативная реализация JCL на примере SLF4J.
SLF4J — более чистая зависимость и более эффективная во время выполнения, чем
commons-logging , потому что он использует привязки времени компиляции
вместо обнаружения других фреймворков во время выполнения
интегрирует. Это также означает, что вы должны более четко указывать, что
вы хотите, чтобы это произошло во время выполнения, и объявите это или настройте его
соответственно. SLF4J обеспечивает привязку ко многим распространенным фреймворкам ведения журналов,
поэтому вы обычно можете выбрать тот, который уже используете, и привязать к нему для
настройка и управление.
SLF4J обеспечивает привязку ко многим распространенным фреймворкам журналирования,
включая JCL, и он также делает обратное: мосты между другими
фреймворки и сам. Итак, чтобы использовать SLF4J с Spring, вам необходимо
Замените зависимость от , ведущую общий журнал, на SLF4J-JCL
мост. Как только вы это сделаете, ведите журнал вызовов из Spring
будут преобразованы в вызовы протоколирования к SLF4J API, поэтому, если другие
библиотеки в вашем приложении используют этот API, тогда у вас будет единое место
для настройки и управления ведением журнала.
Обычным выбором может быть соединение Spring с SLF4J, а затем
обеспечить явную привязку SLF4J к Log4J. Вам нужно поставить 4
зависимости (и исключить существующий commons-logging ):
мост, SLF4J API, привязка к Log4J и Log4J
сама реализация. В Maven вы бы сделали это вот так
<зависимости>
<зависимость>
org.springframework
весенний контекст
<версия> 3.0.0.RELEASE
время выполнения
<исключения>
<исключение>
commons-logging
общедоступное ведение журнала
<зависимость>
org.slf4j
jcl-over-slf4j
<версия> 1.5.8
время выполнения
<зависимость>
org.slf4j
slf4j-api
1.5.8
время выполнения
<зависимость>
org.slf4j
slf4j-log4j12
<версия> 1.5.8
время выполнения
<зависимость>
log4j
log4j
1.2.14
время выполнения
Может показаться, что много зависимостей просто для того, чтобы
Ведение журнала. Ну, это так, но это — это опционально, и это
должен вести себя лучше, чем ванильный commons-logging с
в отношении проблем с загрузчиком классов, особенно если вы находитесь в строгом контейнере
как платформа OSGi.Якобы есть еще и выигрыш в производительности
потому что привязки находятся во время компиляции, а не во время выполнения.
Более распространенный выбор среди пользователей SLF4J, который использует меньше шагов
и генерирует меньше зависимостей, заключается в непосредственной привязке к Logback. Это устраняет лишние
шаг привязки, потому что Logback реализует SLF4J напрямую, поэтому вам нужно только
зависеть от двух библиотек, а не от четырех ( jcl-over-slf4j и
логбэк ). Если вы это сделаете, вам также может потребоваться исключить
зависимость slf4j-api от других внешних зависимостей (не Spring),
потому что вам нужна только одна версия этого API в пути к классам.
Многие люди используют Log4j в качестве логгера.
фреймворк для настройки и управления. Это эффективно
и хорошо зарекомендовавшей себя, и фактически это то, что мы используем во время выполнения, когда мы
собрать и протестировать Spring. Spring также предоставляет некоторые утилиты для
настройка и инициализация Log4j, поэтому у него есть необязательный параметр времени компиляции
зависимость от Log4j в некоторых модулях.
Чтобы заставить Log4j работать с зависимостью JCL по умолчанию
( commons-logging ) все, что вам нужно сделать, это поставить Log4j на
classpath и предоставьте ему файл конфигурации
( log4j.свойства или log4j.xml в корне
пути к классам). Итак, для пользователей Maven это ваша зависимость
декларация:
<зависимости>
<зависимость>
org.springframework
весенний контекст
3.0.0.RELEASE
время выполнения
<зависимость>
log4j
log4j
<версия> 1.2.14
время выполнения
А вот образец log4j.properties для входа в
консоль:
log4j.rootCategory = ИНФОРМАЦИЯ, стандартный вывод
log4j.appender.stdout = org.apache.log4j.ConsoleAppender
log4j.appender.stdout.layout = org.apache.log4j.PatternLayout
log4j.appender.stdout.layout.ConversionPattern =% d {АБСОЛЮТНЫЙ}% 5p% t% c {2}:% L -% m% n
log4j.category.org.springframework.beans.factory = ОТЛАДКА Контейнеры времени выполнения
с собственным JCL
Многие люди запускают свои приложения Spring в контейнере, который
сам предоставляет реализацию JCL.Приложение IBM Websphere
Сервер (WAS) — это архетип. Это часто вызывает проблемы, и
к сожалению, нет решения серебряной пули; просто исключая
commons-logging из вашего приложения недостаточно в
большинство ситуаций.
Чтобы прояснить это: проблемы, о которых сообщают, обычно не
с JCL как таковым, или даже с общего журнала : скорее
они связаны с привязкой общего журнала к другому
framework (часто Log4J). Это может потерпеть неудачу, потому что
commons-logging изменили способ выполнения
открытие между более старыми версиями (1.0) найдено в некоторых
контейнеры и современные версии, которые сейчас используются большинством людей (1.1).
Spring не использует никаких необычных частей JCL API, поэтому ничего
ломается там, но как только Spring или ваше приложение попытается сделать
при любом журналировании вы можете обнаружить, что привязки к Log4J не
за работой.
В таких случаях с WAS проще всего инвертировать
иерархия загрузчика классов (IBM называет ее «родительский последний»), так что
приложение управляет зависимостью JCL, а не контейнером. Что
вариант не всегда открыт, но есть много других предложений
в открытом доступе для альтернативных подходов и вашего пробега
может отличаться в зависимости от конкретной версии и набора функций
контейнер.
Закон Гука и простое гармоническое движение
Объектив
•
для измерения жесткости пружины с помощью закона Гука
•
исследовать статические свойства упругих объектов и пружин, соединенных последовательно и параллельно
•
изучить простой гармонический осциллятор, построенный из пружин и масс
•
чтобы убедиться, что период SHM пропорционален квадратному корню из массы и не зависит от амплитуды
•
для измерения динамической жесткости пружины
•
проверить закон сохранения энергии
Оборудование
Часть I:
•
две почти одинаковые пружины
•
длинная резинка
•
подставка для стойки с измерителем
•
Вешалка для массы 50 г
•
набор масс от 100 г до 600 г
•
шкала баланса
•
Интерфейс научной мастерской с датчиком силы и детектором вращательного движения, используемым в качестве линейного датчика
Часть II:
•
столкновение тележки известной массы на горизонтальной динамической дорожке, колеблющейся посредством параллельных пружин
•
датчик движения и фотозатвор, подключенный к интерфейсу Science Workshop
•
нелинейные упругие предметы (резинки)
•
два прямоугольных груза ~ 0.По 5 кг для изменения массы системы
Введение и теория
Закон Гука
Сила упругости возникает в пружине, когда пружина растягивается / сжимается или деформируется (Δx) под действием внешней силы. Сила упругости действует в направлении, противоположном внешней силе. Он пытается привести деформированный конец пружины в исходное (равновесное) положение. См. Рис. 1.
Рисунок 1
Если растяжение относительно невелико, величина силы упругости прямо пропорциональна растяжению Δx согласно закону Гука:
где k — постоянная, обычно называемая жесткостью пружины, а Δx — растяжение (разница между новым ( x ) и положением равновесия).Знак минус перед жесткостью пружины в уравнении 1
F el = -kΔx
указывает, что сила упругости и растяжение действуют в противоположном направлении.
Простое гармоническое движение
Если висящую массу сместить из положения равновесия и отпустить, то произойдет простое гармоническое движение (SHM). SHM означает, что положение изменяется с синусоидальной зависимостью от времени.
(2)
x = X макс cos ( ω т)
Ниже приведены уравнения для скорости и ускорения.
(3)
v = −X макс ω sin ( ω t)
(4)
a = −X макс ω 2 cos ( ω t)
Подставляя уравнения 2
x = X max cos ( ω t)
, 4
a = −X max ω 2 cos ( ω t)
и 1
F el = −kΔx
во Второй закон Ньютона, можно вывести уравнение для угловой резонансной частоты колебательной системы:
(5)
ω =
где k — жесткость пружины, а m — масса системы, совершающей простое гармоническое движение.Единица угловой частоты
радиана в секунду = рад / с.
Собственную резонансную частоту осциллятора можно изменить, изменив жесткость пружины или колеблющуюся массу. Использование более жесткой пружины увеличит частоту колебательной системы. Добавление массы в систему уменьшило бы ее резонансную частоту.
Двумя другими важными характеристиками колебательной системы являются период ( T ) и линейная частота ( f ). Период колебаний — это время, за которое объект совершает одно колебание.Линейная частота — это количество колебаний в секунду. Период обратно пропорционален линейной частоте.
Единицей измерения периода является секунда (с), а единицей измерения частоты — Герц или с –1 (Гц = 1 / с).
Угловая частота связана с периодом и линейной частотой согласно следующему выражению.
Энергия
Для возникновения колебаний в систему должна быть передана энергия. Когда объект выходит из равновесия, в системе накапливается упругая потенциальная энергия.После того, как объект выпущен, потенциальная энергия трансформируется в кинетическую энергию и обратно. В гармоническом осцилляторе происходит непрерывное переключение между потенциальной и кинетической энергией.
Для колеблющейся пружины ее потенциальная энергия ( E p ) в любой момент времени равна работе ( W ), проделанной при растяжении пружины до соответствующего смещения x .
Кинетическая энергия ( E k ) осциллятора в любой момент времени будет соответствовать хорошо известному уравнению:
Соответственно можно рассчитать максимальную потенциальную энергию и максимальную кинетическую энергию.Согласно закону сохранения энергии: «Механическая энергия сохраняется (не разрушается и не создается) в колебательной системе без трения».
Процедура
Распечатайте лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.
Часть I — Закон Гука
Измерение жесткости пружины, метод 1
Целью этой части лабораторных работ является определение жесткости пружины. Жесткость пружины — это коэффициент пропорциональности между силой упругости и смещением в соответствии с законом Гука (уравнение 1
F el = −kΔx
).
1
Подвесьте пружину к опоре, добавьте весовую подвеску, измерьте исходное положение равновесия с помощью измерительной линейки и запишите его.
2
Добавляйте гири с шагом от 100 г до 600 г и измеряйте соответствующее положение.
3
Обсудите с членами вашей группы столбцы, которые необходимо подготовить в GA для записи данных. Составьте черновик таблицы и сверьте его со своим техническим специалистом. Подготовьте столбцы в GA.
4
Создайте новый расчетный столбец для данных силы упругости (ДАННЫЕ → НОВАЯ РАСЧЕТНАЯ КОЛОННА → уравнение: F = переменные « м » * г , где м в кг).
5
Создайте новый вычисляемый столбец для смещения (ДАННЫЕ → НОВЫЙ РАСЧЕТНЫЙ КОЛОНК → уравнение = переменные «положение» — начальное положение равновесия).
6
Постройте график зависимости силы от смещения.
7
Запишите наклон графика и его погрешность в Рабочую таблицу лабораторной работы 8. Вы будете использовать значение наклона и его неопределенность, чтобы найти жесткость пружины и ее погрешность.
Измерение жесткости пружины, метод 2
Схема установки, показанная на рис.2 будет использоваться для определения жесткости пружины 2.
Рисунок 2 : Аппаратная установка для эксперимента по закону Гука
1
Откройте предварительно установленный файл эксперимента: desktop \ pirt-labs \ phy 113 \ PreSetUpFiles \ Springs.
2
Перед получением фактических данных откалибруйте датчик силы. Нажмите кнопку «Настройка» на панели инструментов. Затем щелкните значок датчика силы и нажмите кнопку «Калибровать датчики». Появится панель калибровки, показанная на рис.3.
Рисунок 3 : Калибровка датчика силы в Data Studio
Параметр «2 точки» должен быть выбран в качестве «Тип калибровки». При отсутствии нагрузки на датчик силы введите 0 в окне стандартных значений «Точка калибровки 1». Нажимаем кнопку «Тарирование» на датчике силы. Это действие сбрасывает показания датчика силы на ноль. Нажмите кнопку «Считать с датчика». Затем повесьте крюк весом 1 кг на датчик и введите 9.8 в окне стандартных значений «Точка калибровки 2».Нажмите кнопку «Считать с датчика». Нажмите «ОК», чтобы сохранить эту калибровку. Закройте окна «Калибровка датчиков» и «Настройка». Теперь вы готовы к фактическим измерениям жесткости пружины.
3
Замените груз весом 1 кг на пружину. Прикрепите к нему кусок веревки. Оберните шнур вокруг большого шкива детектора вращательного движения против часовой стрелки, как показано на рис. 2. Датчик вращательного движения откалиброван для считывания линейного расстояния.
4
Нажмите кнопку «Старт», чтобы начать сбор данных. Осторожно потяните за шнур, наблюдая за окном дисплея Force. Начните отпускать струну, когда сила достигнет 10 Н.
5
Примените линейную аппроксимацию к хорошей части вашей записи (см. Рис. 4), которая представляет график зависимости силы упругости от смещения. Наклон этой линии дает жесткость пружины.
6
Запишите наклон графика «Сила против зелья» и его неопределенность в Рабочем листе Лаборатории 8.Вы будете использовать значение наклона и его неопределенность, чтобы найти жесткость пружины и ее погрешность.
7
Повторите эту процедуру для системы пружин, включенных последовательно и параллельно.
8
Запишите наклон графика силы и положения и его погрешность в Рабочую таблицу лабораторной работы 8. Вы будете использовать значение наклона и его неопределенность, чтобы найти жесткость пружины и ее погрешность. В разделе «Обсуждение» вам нужно будет сравнить значение жесткости пружины для системы пружин со значением каждой жесткости пружины.
Рисунок 4 : Образец файла эксперимента в DataStudio
Исследование нелинейного упругого объекта.
1
В экспериментальной установке на рис. 2, замените пружину длинной резинкой.
2
Запишите силу по отношению к положению как для движений вниз (увеличение силы), так и движений вверх (уменьшение силы).
Часть II — Простое гармоническое движение
В этой части эксперимента вы проверите, зависит ли период от амплитуды; рассчитать резонансную частоту и жесткость пружины системы.Вы запишите собранные данные в рабочий лист лабораторной работы 8.
1
Настройте эксперимент, как показано на рисунках ниже. Откройте файл предустановленного эксперимента: desktop \ pirt-labs \ phy 113 \ PreSetUpFiles \ SHM.
Рисунок 5
Рисунок 6
2
Без дополнительной массы измерьте период колебаний для начальных амплитуд 4 см и 12 см. Сбор данных автоматически прекратится через 5 секунд.Пример записи показан на рис. 2. Период измеряется фотозатвором и записывается в таблице 1 слева от графика.
3
Без дополнительной массы переместите тележку из положения равновесия примерно на 8 см и начните запись. Снова запишите период колебаний тележки, измеренный фотозатвором. Запишите все три периода колебаний в Рабочем листе Лаборатории 8.
Рисунок 7 : Пример файла для эксперимента SHM в DataStudio
4
Установите запись положения vs.время до синусоиды. Параметр А — амплитуда (максимальное смещение) колебаний. Параметр B дает вам период колебаний. Вы можете сравнить его значение со значением периода, измеренного фотозатвором. Параметр D — положение равновесия. Используйте параметр B для расчета резонансной частоты и жесткости пружины системы с помощью уравнений 7 и 5 ω =
из раздела «Введение и теория» в этом руководстве по лабораторной работе.
5
Подгоните запись скорости относительно времени к синусоиде. Запишите параметр A — амплитуду (максимальное значение) графика зависимости скорости от времени.
Обратите внимание, что оба графика, положение в зависимости от времени и скорость в зависимости от времени, представляют собой периодические волны одной и той же частоты, только смещенные на 90 °. Максимальное и минимальное значения положения возникают, когда скорость равна нулю, а также максимальные и минимальные значения. скорости происходят, когда положение находится в равновесии.
Что касается энергии системы, это означает, что когда потенциальная энергия максимальна (максимальное смещение), кинетическая энергия равна нулю.В этот момент энергия полностью потенциальна. Точно так же в точке, когда пружина не растянута (объект проходит точку равновесия), вся энергия является кинетической.
Чтобы проверить теорему сохранения энергии для колеблющейся тележки, достаточно сравнить ее максимальную потенциальную энергию с максимальной кинетической энергией, найдя процентную разницу потерь энергии.
Связь между периодом и массой
Это часть эксперимента, в которой вы убедитесь, что период SHM пропорционален квадратному корню из массы.
1
Загрузите тележку тяжелыми грузами (по одной) и измерьте период SHM, сохраняя при этом постоянную амплитуду, например 8 см.
2
Включая данные из предыдущей части эксперимента, у вас будет три точки, чтобы построить график периода против
| м |
. Согласно теории (уравнения 5 ω =
и 7) этот график должен быть прямой линией.
3
Запишите наклон графика T по сравнению с
| м |
в Рабочем листе Лаборатории 8.
4
Используйте значение наклона и его неопределенность, чтобы найти жесткость пружины.
5
На основании наклона графика рассчитайте динамическую жесткость пружины системы.
Подсказка: Подстановка
в
ω =
дает
=
.
Решение относительно T дает следующее.
T =
2 π k м
Обсуждение
Укажите цель лаборатории. Сравните экспериментальные результаты жесткости пружины для одиночной пружины из методов 1 и 2 с их теоретическими значениями.Какая разница в процентах? Как жесткость пружины для системы из двух последовательно соединенных пружин связана с жесткостью отдельных пружин? Как жесткость пружины для системы из двух параллельно включенных пружин связана с жесткостью отдельных пружин? Все ли весенние объекты подчиняются закону Гука?
Какой вывод можно сделать о связи периода и амплитуды на основании собранных данных? Согласованы ли измерения жесткости пружины друг с другом? Был ли соблюден закон сохранения энергии в вашем эксперименте? Исходя из ваших экспериментальных данных, какова связь между периодом колебаний и массой в системе пружина-масса? Объясните, какую физическую величину можно принять за характеристику колебательной системы.Обобщите основные характеристики простого гармонического движения.
Заключение
Вы достигли цели лаборатории?
Copyright © 2012 Advanced Instructional Systems Inc. и факультет физики Университета штата Аризона | Кредиты
Зависимый от использования блок рецептора AMPA у мышей, лишенных GluR2, предполагает постсинаптический сайт для экспрессии LTP
Bliss, T.V. & Collingridge, G.L. Синаптическая модель памяти: долгосрочное потенцирование в гиппокампе. Nature 361 , 31–39 (1993).
CAS
Статья
Google Scholar
Malinow, R. & Tsien, R. W. Пресинаптическое усиление, показанное с помощью записи долгосрочной потенциации целых клеток в срезах гиппокампа. Nature 346 , 177–180 (1990).
CAS
Статья
Google Scholar
Куллманн, Д. М. и Николл, Р.A. Долгосрочная потенциация связана с увеличением квантового содержания и квантовой амплитуды. Nature 357 , 240–244 (1992).
CAS
Статья
Google Scholar
Larkman, A., Hannay, T., Stratford, K. & Jack, J. Вероятность пресинаптического высвобождения влияет на локус долгосрочной потенциации. Nature 360 , 70–73 (1992).
CAS
Статья
Google Scholar
Ляо, Д., Джонс, А. и Малинов, Р. Прямое измерение количественных изменений, лежащих в основе долгосрочной потенциации в гиппокампе CA1. Нейрон 9 , 1089–1097 (1992).
CAS
Статья
Google Scholar
Стивенс, К. Ф. и Ван, Ю. Изменения надежности синаптической функции как механизма пластичности. Nature 371 , 704–707 (1994).
CAS
Статья
Google Scholar
Большаков, В.Y. & Siegelbaum, S.A. Регуляция высвобождения медиатора в гиппокампе во время развития и долгосрочной потенциации. Наука 269 , 1730–1734 (1995).
CAS
Статья
Google Scholar
Фостер, Т. К. и Макнотон, Б. Л. Долгосрочное усиление синаптической передачи СА1 происходит из-за увеличения квантового размера, а не количественного содержания. Гиппокамп 1 , 79–91 (1991).
CAS
Статья
Google Scholar
Манабэ, Т., Реннер, П. и Николл, Р. А. Постсинаптический вклад в долговременную потенциацию выявлен анализом миниатюрных синаптических токов. Nature 355 , 50–55 (1992).
CAS
Статья
Google Scholar
Ляо, Д., Хесслер, Н. А. и Малинов, Р. Активация постсинаптически молчаливых синапсов во время индуцированного спариванием LTP в области CA1 среза гиппокампа. Nature 375 , 400–404 (1995).
CAS
Статья
Google Scholar
Исаак, Дж. Т., Николл, Р. А. и Маленка, Р. С. Доказательства молчания синапсов: значение для экспрессии LTP. Нейрон 15 , 427–434 (1995).
CAS
Статья
Google Scholar
Isaac, J. T., Hjelmstad, G.O., Nicoll, R.A. & Malenka, R.C. Долгосрочная потенциация на входе одного волокна в пирамидные клетки CA1 гиппокампа. Proc. Natl. Акад. Sci. США 93 , 8710–8715 (1996).
CAS
Статья
Google Scholar
Стрикер К., Филд А. С. и Редман С. Дж. Изменения квантовых параметров EPSC в нейронах СА1 крысы in vitro после индукции длительной потенциации. J. Physiol. (Лондон) 490 , 443–454 (1996).
CAS
Статья
Google Scholar
Куллманн, Д.М. Колебания амплитуды двухкомпонентных EPSC в пирамидных клетках гиппокампа: последствия для долгосрочной потенциации. Нейрон 12 , 1111–1120 (1994).
CAS
Статья
Google Scholar
Дюран, Г. М., Ковальчук, Ю. и Коннерт, А. Долгосрочная потенциация и функциональная индукция синапсов в развивающемся гиппокампе. Nature 381 , 71–75 (1996).
CAS
Статья
Google Scholar
Куллманн, Д.М., Эрдемли, Г. и Астели, Ф. LTP сигналов, опосредованных рецептором AMPA и NMDA: доказательства пресинаптической экспрессии и внесинаптического распространения глутамата. Нейрон 17 , 461–474 (1996).
CAS
Статья
Google Scholar
Астели, Ф., Эрдемли, Г. и Куллманн, Д. М. Внесинаптическое распространение глутамата в гиппокампе: зависимость от температуры и роль активного поглощения глутамата. Нейрон 18 , 281–293 (1997).
CAS
Статья
Google Scholar
Линч, Г. и Бодри, М. Биохимия памяти: новая и конкретная гипотеза. Наука 224 , 1057–1063 (1984).
CAS
Статья
Google Scholar
Марен, С., Токко, Г., Стэндли, С., Бодри, М. и Томпсон, Р.F. Постсинаптические факторы в экспрессии долгосрочной потенциации (LTP): усиление связывания рецептора глутамата после индукции LTP in vivo. Proc. Natl. Акад. Sci. США 90 , 9654–9658 (1993).
CAS
Статья
Google Scholar
Амброс-Ингерсон, Дж. И Линч, Дж. Кинетика стробирования канала и синаптическая эффективность: гипотеза для выражения долгосрочной потенциации. Proc. Natl. Акад.Sci. США 90 , 7903–7907 (1993).
CAS
Статья
Google Scholar
Рош, К. В., Тингли, В. Г. и Хуганир, Р. Л. Фосфорилирование глутаматного рецептора и синаптическая пластичность. Curr. Opin. Neurobiol. 4 , 383–388 (1994).
CAS
Статья
Google Scholar
Бенке, Т. А., Андерсон, В. В. и Коллингридж, Г.Проводимость канала рецептора L. AMPA повышена в области LTP CA1 гиппокампа крысы. Nature 393 , 793–797 (1998).
CAS
Статья
Google Scholar
Hessler, N. A., Shirke, A. M. & Malinow, R. Вероятность высвобождения медиатора в центральном синапсе млекопитающих. Nature 366 , 569–572 (1993).
CAS
Статья
Google Scholar
Розенмунд, К., Клементс, Дж. Д. и Вестбрук, Г. Л. Неоднородная вероятность высвобождения глутамата в синапсе гиппокампа. Science 262 , 754–757 (1993).
CAS
Статья
Google Scholar
Manabe, T. и Nicoll, R.A. Долгосрочная потенциация: доказательства против увеличения вероятности высвобождения медиатора в области CA1 гиппокампа. Наука 265 , 1888–1892 (1994).
CAS
Статья
Google Scholar
Уошберн М.С. и Дингледин Р. Блокирование рецепторов альфа-амино-3-гидрокси-5-метил-4-изоксазолепропионовой кислоты (AMPA) полиаминами и токсинами полиаминов . J. Pharmacol. Exp. Ther. 278 , 669–678 (1996).
CAS
PubMed
Google Scholar
Bahring R. & Mayer, M. L. Анализ филантротоксинового блока для рекомбинантных каналов рецепторов глутамата крысиного GluR6 (Q). J. Physiol. (Лондон) (в печати).
Washburn, M. S., Numberger, M. Zhang, S. & Dingledine, R. Дифференциальная зависимость от экспрессии GluR2 трех характерных особенностей рецепторов AMPA. J. Neurosci. 17 , 9393–9406 (1998).
Артикул
Google Scholar
Jia, Z. et al. Повышенный LTP у мышей с дефицитом рецептора AMPA GluR2. Нейрон 17 , 945–956 (1996).
CAS
Статья
Google Scholar
Malgaroli, A. et al. Пресинаптический компонент долговременной потенциации, визуализируемый в отдельных синапсах гиппокампа. Наука 268 , 1624–1628 (1995).
CAS
Статья
Google Scholar
Хуанг, Э. П. и Стивенс, К. Ф. Оценка распределения синаптической надежности. J. Neurophysiol. 78 , 2870–2880 (1997).
CAS
Статья
Google Scholar
Добрунц, Л. Э. и Стивенс, К. Ф. Неоднородность вероятности высвобождения, облегчения и истощения центральных синапсов. Нейрон 18 , 995–1008 (1997).
CAS
Статья
Google Scholar
Исааксон, Дж. С. и Николл, Р.A. Анирацетам снижает десенсибилизацию рецептора глутамата и замедляет затухание быстрых возбуждающих синаптических токов в гиппокампе. Proc. Natl. Акад. Sci. США 88 , 10936–10940 (1991).
CAS
Статья
Google Scholar
Тан, К. М., Ши, К. Ю., Катчман, А. и Линч, Г. Модуляция динамики быстрых EPSC и кинетики глутаматных каналов с помощью анирацетама. Science 254 , 288–290 (1991).
CAS
Статья
Google Scholar
Партин, К. М., Флек, М. В. и Майер, М. Л. Флип / флоп-мутанты рецептора AMPA, влияющие на дезактивацию, десенсибилизацию и модуляцию циклотиазидом, анирацетамом и тиоцианатом. Дж. Neurosci . 16 , 6634–6647 (1996).
CAS
Статья
Google Scholar
Traynelis, S. F. & Wahl, P.Контроль вероятности открытия глутаматного рецептора GluR6 крысы протеинкиназой А и кальциневрином. J. Physiol. (Лондон) 503 , 513–531 (1997).
CAS
Статья
Google Scholar
Greengard, P., Jen, J., Nairn, A.C. & Stevens, C.F. Усиление глутаматного ответа с помощью цАМФ-зависимой протеинкиназы в нейронах гиппокампа. Наука 253 , 1135–1138 (1991).
CAS
Статья
Google Scholar
Ву, Г., Малинов, Р. и Клайн, Х. Т. Созревание центрального глутаматергического синапса. Наука 274 , 972–976 (1996).
CAS
Статья
Google Scholar
Спейсек, Дж. И Харрис, К. М. Трехмерная организация гладкой эндоплазматической сети в дендритах СА1 гиппокампа и дендритных шипах незрелой и зрелой крысы. J. Neurosci. 17 , 190–203 (1997).
CAS
Статья
Google Scholar
Льедо, П.М., Чжан, X., Судхоф, Т.С., Маленка, Р.С., Николл, Р.А. Постсинаптическое слияние мембран и долгосрочное потенцирование. Наука 279 , 399–403 (1998).
CAS
Статья
Google Scholar
Константин-Патон, М. и Клайн, Х. Т. LTP и зависимый от активности синаптогенез: чем больше они похожи, тем более разными они становятся. Curr. Opin. Neurobiol. 8 , 139–148 (1998).
CAS
Статья
Google Scholar
Лисман, Дж., Маленка, Р. К., Николл, Р. А. и Малинов, Р. Механизмы обучения: пример CaM-KII. Наука 276 , 2001–2002 (1997).
CAS
Статья
Google Scholar
Maletic-Savatic, M., Koothan, T. и Malinow, R. Вызванный кальцием дендритный экзоцитоз в культивируемых нейронах гиппокампа.Часть II: посредничество кальций / кальмодулин-зависимой протеинкиназы II. J. Neurosci. 18 , 6814–6821 (1998).
CAS
Статья
Google Scholar
Ширке А. М. и Малинов Р. Механизмы потенцирования кальций-кальмодулиновой киназой II постсинаптической чувствительности в нейронах СА1 гиппокампа крысы. J. Neurophysiol. 78 , 2682–2692 (1997).
CAS
Статья
Google Scholar
Нисимунэ, А. et al. Связывание NSF с GluR2 регулирует синаптическую передачу. Нейрон 21 , 87–97 (1998).
CAS
Статья
Google Scholar
Nayak, A., Zastrow, D. J., Licksteig, R., Zahniser, N. R., Browning, M. D. Поддержание поздней фазы LTP сопровождается PKA-зависимым увеличением синтеза рецептора AMPA. Nature 394 , 680–683 (1998).
CAS
Статья
Google Scholar
Ван, Кв.и другие. Рекрутирование функциональных рецепторов ГАМК (А) в постсинаптические домены инсулином. Nature 388 , 686–690 (1997).
CAS
Статья
Google Scholar
| Осенний блок I 2021 6 недель | Крайний срок пройден | 16 августа 2021 г. | 25 сен.2021 | 5 950 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 4533 долларов США Жилье = 950 $ Страховка = 167 $ Общая комиссия = 5 950 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 900 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 200 $ Книги и расходные материалы = 100 $ Личные расходы = 1000 долларов Прочие = 161 $ Общая сметная стоимость = 3611 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Осенние блоки I, II 2021 12 недель | Крайний срок пройден | 16 августа 2021 г. | 6 нояб.2021 г. | 11 900 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 9 533 долларов США Жилье = 1900 долларов Страховка = 167 $ Общие сборы = 11 900 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 1,800 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 400 $ Книги и расходные материалы = 200 $ Личные расходы = 2000 долларов Прочие = 161 $ Общая сметная стоимость = 5 811 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Осенние блоки I, II, III 2021 г. 18 недель | Крайний срок пройден | 16 августа 2021 г. | 18 декабря 2021 г. | 17 850 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 14 533 долларов США Жилье = 2 850 долларов США Страховка = 167 $ Общие сборы = 17 850 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 2700 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 600 $ Книги и расходные материалы = 300 $ Визовый сбор = 360 долларов Личные расходы = 3000 долларов Прочие = 161 $ Общая сметная стоимость = 8 371 доллар США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Осенний блок II 2021 6 недель | Крайний срок пройден | 27 сен.2021 | 6 нояб.2021 г. | 5 950 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 4533 долларов США Жилье = 950 $ Страховка = 167 $ Общая комиссия = 5 950 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 900 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 200 $ Книги и расходные материалы = 100 $ Личные расходы = 1000 долларов Прочие = 161 $ Общая сметная стоимость = 3611 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Осенние блоки II, III 2021 г. 12 недель | Крайний срок пройден | 27 сен.2021 | 18 декабря 2021 г. | 11 900 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 9 533 долларов США Жилье = 1900 долларов Страховка = 167 $ Общие сборы = 11 900 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 1,800 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 400 $ Книги и расходные материалы = 200 $ Личные расходы = 2000 долларов Прочие = 161 $ Общая сметная стоимость = 5 811 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Осенний блок III 2021 6 недель | Крайний срок пройден | 8 нояб.2021 г. | 18 декабря 2021 г. | 5 950 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 4533 долларов США Жилье = 950 $ Страховка = 167 $ Общая комиссия = 5 950 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 900 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 200 $ Книги и расходные материалы = 100 $ Личные расходы = 1000 долларов Прочие = 161 $ Общая сметная стоимость = 3611 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| OC 2021-2022 учебный год 38 недель | Крайний срок пройден | 16 августа 2021 г. | 7 мая 2022 г. | 36 600 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 600 $ Затраты на образование = 26 576 долларов США Жилье = 9 090 долларов США Страховка = 334 $ Общие сборы = 36 600 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 5400 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 1250 долларов США Книги и расходные материалы = 600 $ Визовый сбор = 450 долларов Личные расходы = 6200 долларов Прочие = 161 $ Расходы в перерыве = 900 $ Общая сметная стоимость = 16 211 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Весенний блок I 2022 6 недель | 1 ноя.2021 г. | 3 янв.2022 г. | 12 февраля 2022 г. | 6250 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 4833 долларов США Жилье = 950 $ Страховка = 167 $ Общая комиссия = 6250 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 900 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 250 $ Книги и расходные материалы = 100 $ Личные расходы = 1200 $ Прочие = 161 $ Общая сметная стоимость = 3861 доллар США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Пружинные блоки I, II 2022 г. 12 недель | 1 ноя.2021 г. | 3 янв.2022 г. | 26 марта 2022 г. | 12 500 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 10 133 доллара США Жилье = 1900 долларов Страховка = 167 $ Общие сборы = 12 500 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 1,800 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 450 $ Книги и расходные материалы = 200 $ Личные расходы = 2200 долларов Прочие = 161 $ Общая сметная стоимость = 6061 доллар США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Пружинные блоки I, II, III 2022 г. 18 недель | 1 ноя.2021 г. | 3 янв.2022 г. | 7 мая 2022 г. | 18 750 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 15 433 долларов США Жилье = 2 850 долларов США Страховка = 167 $ Общая комиссия = 18 750 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 2700 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 650 $ Книги и расходные материалы = 300 $ Визовый сбор = 450 долларов Личные расходы = 3200 долларов Прочие = 161 $ Общая сметная стоимость = 8 711 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Весенний блок II 2022 6 недель | 1 ноя.2021 г. | 14 февраля 2022 г. | 26 марта 2022 г. | 6250 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 4833 долларов США Жилье = 950 $ Страховка = 167 $ Общая комиссия = 6250 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 900 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 200 $ Книги и расходные материалы = 100 $ Личные расходы = 1000 долларов Прочие = 161 $ Общая сметная стоимость = 3611 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Пружинные блоки II, III 2022 г. 12 недель | 1 ноя.2021 г. | 14 февраля 2022 г. | 7 мая 2022 г. | 12 500 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 10 133 доллара США Жилье = 1900 долларов Страховка = 167 $ Общие сборы = 12 500 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 1,800 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 400 $ Книги и расходные материалы = 200 $ Личные расходы = 2000 долларов Прочие = 161 $ Общая сметная стоимость = 5 811 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
| Пружинный блок III 2022 6 недель | 1 ноя.2021 г. | 28 марта 2022 г. | 7 мая 2022 г. | 6250 долл. США Нажмите, чтобы закрыть Стоимость программыCIEE предлагает максимальную поддержку студентов из всех провайдеров в рамках своей платы за программу, включая приветствие в аэропорту, постоянное руководство и поддержку, ориентацию, культурные мероприятия, местные экскурсии, консультации перед отъездом и страхование путешествий CIEE iNext с льготами. Подтверждение участия = 300 $ Затраты на образование = 4833 долларов США Жилье = 950 $ Страховка = 167 $ Общая комиссия = 6250 долларов США. Сметная стоимостьСтуденты несут ответственность и управляют расходами, связанными с поездками, питанием, книгами и личными расходами.Ниже приведены оценки для рассмотрения. Питание не включено в стоимость программы = 900 $ Международные авиабилеты = 1250 долларов США Местный транспорт = 200 $ Книги и расходные материалы = 100 $ Личные расходы = 1000 долларов Прочие = 161 $ Общая сметная стоимость = 3611 долларов США. Финансовая помощьCIEE предлагает наибольшее количество грантов и стипендий среди любой организации, обучающейся за рубежом, включая гранты на поездки в размере 8 миллионов долларов в год, стипендии на основе заслуг, институциональные гранты и гранты MSI, а также глобальные гранты Gilman Go. См. Стипендии |
Как вычесть расходы на образование
Расходы на образование, связанное с работой
Если вы являетесь сотрудником, вы можете вычесть из стоимости обучения следующую сумму:
- Поддерживает или улучшает навыки, необходимые для вашей нынешней работы
- Требуется вашим работодателем
Вы не можете вычесть расходы на обучение, если курс:
- Не имеет отношения к вашей работе
- Подходит для новой профессии или профессии
- Требуется для соответствия минимальным образовательным требованиям, действовавшим на момент вашего первого приема на работу
Чтобы вычесть их, перечислите вычеты в таблице А.Ваши вычеты должны превышать 2% порогового значения скорректированного валового дохода (AGI) для разных вычетов.
Расходы на образование, связанные с работой, также могут дать вам право на получение других налоговых льгот, например:
- Американский кредит возможностей
- Кредит на пожизненное обучение
Кроме того, эти расходы могут дать вам право требовать более одной налоговой льготы. Если вы используете разные расходы для расчета каждого пособия, вы обычно можете требовать столько пособий, сколько захотите.
Расходы на образование и самозанятость
Если вы работаете не по найму, вы можете вычесть стоимость обучения для вашей профессии или бизнеса в Приложении C. Вы должны иметь возможность доказать, что курс:
- Поддерживает или улучшает навыки, необходимые вам в торговле или бизнесе
- Требуется законом или постановлением для сохранения вашей лицензии на занятие своей профессией или профессией
Вы не можете вычесть понесенные вами расходы на образование:
- Для удовлетворения минимальных требований вашей нынешней торговли или бизнеса
- Это дает вам право на новую профессию или бизнес
Это верно, даже если образование поддерживает или улучшает навыки, необходимые в настоящее время в вашем бизнесе.
Допустимые расходы
Вы можете вычесть:
- Стоимость обучения, учебники и сборы
- Оборудование и другие расходы, связанные с получением образования — Пример: вы можете вычесть расходы на исследования и набор текста, которые вы понесли при написании работы для класса.
- Транспортные расходы — вы можете вычесть стоимость проезда между вашим местом работы и школой. Если вы вернетесь на работу после занятий, вы можете вычесть расходы на поездку туда и обратно. Вы также можете вычесть расходы на общественный транспорт.
Невозможно вычесть:
- Путешествие как форма обучения — Пример: учитель испанского языка, который едет в Испанию, чтобы улучшить свои знания испанского языка, не может вычесть свои командировочные расходы.
- Стоимость отпуска или ежегодного отпуска, взятого вами для посещения занятий, в долларах
Многие вычитаемые расходы на образование, связанные с работой, могут иметь право на получение других образовательных кредитов или вычетов.

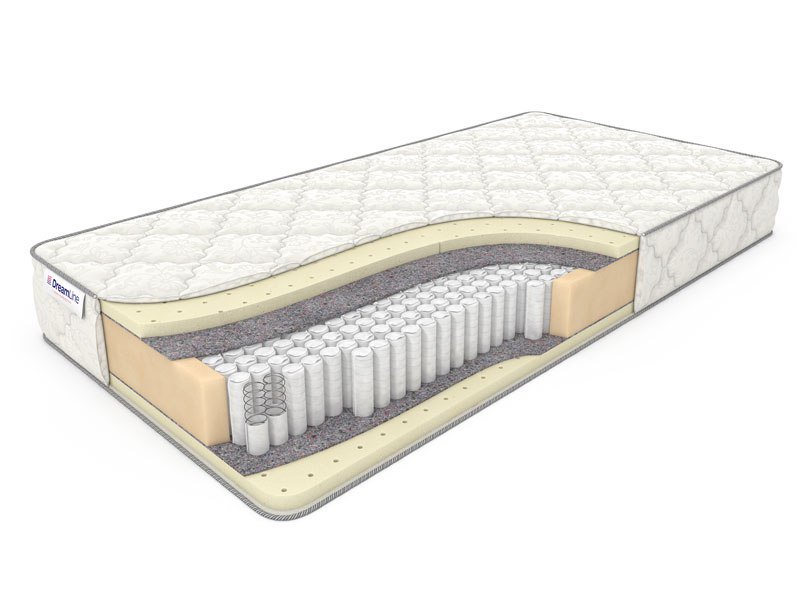 Чем более совершенный блок в модели, тем лучше он к ней адаптируется, и тем больший вес он выдерживает.
Чем более совершенный блок в модели, тем лучше он к ней адаптируется, и тем больший вес он выдерживает. Скрутка никак не влияет на его характеристики. Обратите внимание — скрученный на производстве матрас скрутить обратно получится только с помощью специального пресса!
Скрутка никак не влияет на его характеристики. Обратите внимание — скрученный на производстве матрас скрутить обратно получится только с помощью специального пресса! Пружинные блоки Боннель не выдерживают массу свыше 90-120 кг. В редких случаях производителям удается увеличить их выносливость, но таких матрасов ощутимо меньше, и стоят они дороже.
Пружинные блоки Боннель не выдерживают массу свыше 90-120 кг. В редких случаях производителям удается увеличить их выносливость, но таких матрасов ощутимо меньше, и стоят они дороже.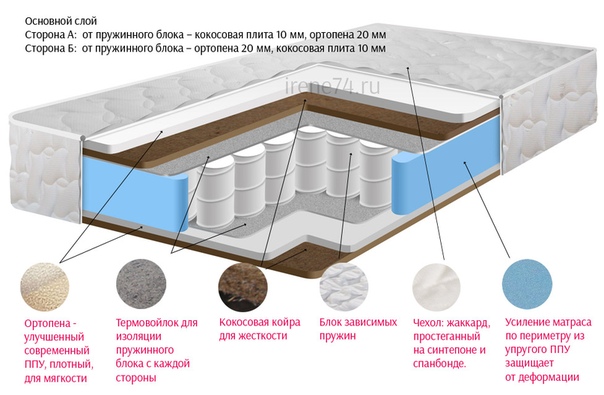 Например, бедра или плечи. Зональный блок усилен (больше витков проволоки, либо утолщенный профиль) в этих зонах. Такие модели рекомендуют людям с большим весом.
Например, бедра или плечи. Зональный блок усилен (больше витков проволоки, либо утолщенный профиль) в этих зонах. Такие модели рекомендуют людям с большим весом. Таким образом производители улучшают ортопедические характеристики матрасов, делают их выносливее. Использование ППУ положительно скажется на долговечности матраса в целом. Такие пружины есть у Light Way и Hönnemed.
Таким образом производители улучшают ортопедические характеристики матрасов, делают их выносливее. Использование ППУ положительно скажется на долговечности матраса в целом. Такие пружины есть у Light Way и Hönnemed. Наиболее популярная разновидность блока. Состоит из 6-витковых пружин в виде бочонка количеством до 300 штук на квадратный метр. Обладает выраженными ортопедическими свойствами.
Наиболее популярная разновидность блока. Состоит из 6-витковых пружин в виде бочонка количеством до 300 штук на квадратный метр. Обладает выраженными ортопедическими свойствами. Рекомендован для пар с большой разницей в весе и обладателям солидной массы тела.
Рекомендован для пар с большой разницей в весе и обладателям солидной массы тела. Данную особенность любят использовать в рекламе, ставя бокал с вином на матрас и прыгая рядом с ним. Бокал не разливается, потому что нету жёсткой зависимости между местом куда применили силу и там где стоит бокал.
Данную особенность любят использовать в рекламе, ставя бокал с вином на матрас и прыгая рядом с ним. Бокал не разливается, потому что нету жёсткой зависимости между местом куда применили силу и там где стоит бокал. Замена составит от 4 до 7 т.р. в зависимости от производителя.
Замена составит от 4 до 7 т.р. в зависимости от производителя.
 Период T и частота f простого гармонического осциллятора задаются выражениями [latex] T = 2 \ pi \ sqrt {\ frac {m} {k}} \\ [/ latex] и [latex] f = \ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}} \\ [/ latex], где м — масса системы.
Период T и частота f простого гармонического осциллятора задаются выражениями [latex] T = 2 \ pi \ sqrt {\ frac {m} {k}} \\ [/ latex] и [latex] f = \ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}} \\ [/ latex], где м — масса системы.
 50 с. Какую массу нужно добавить к объекту, чтобы изменить период до 2,00 с?
50 с. Какую массу нужно добавить к объекту, чтобы изменить период до 2,00 с? 00 Гц. Доска имеет полезную массу 10,0 кг. Какова частота простого гармонического движения дайвера весом 75,0 кг на доске?
00 Гц. Доска имеет полезную массу 10,0 кг. Какова частота простого гармонического движения дайвера весом 75,0 кг на доске? army.mil)
army.mil)